இந்த பாடத்தில் விண்வெளியில் இணையான கோடுகள் என்ற தலைப்பில் அடிப்படை வரையறைகள் மற்றும் கோட்பாடுகளை வழங்குவோம்.
பாடத்தின் தொடக்கத்தில், விண்வெளியில் இணையான கோடுகளின் வரையறையைப் பரிசீலிப்போம் மற்றும் விண்வெளியில் எந்தப் புள்ளியிலும் கொடுக்கப்பட்ட ஒன்றிற்கு இணையாக ஒரு கோடு மட்டுமே வரைய முடியும் என்ற தேற்றத்தை நிரூபிப்போம். அடுத்து நாம் ஒரு விமானத்தை வெட்டும் இரண்டு இணையான கோடுகள் பற்றி லெம்மாவை நிரூபிக்கிறோம். அதன் உதவியுடன் மூன்றாவது வரிக்கு இணையான இரண்டு கோடுகள் பற்றிய தேற்றத்தை நிரூபிப்போம்.

தலைப்பு: கோடுகள் மற்றும் விமானங்களின் இணையான தன்மை

பாடம்: விண்வெளியில் இணையான கோடுகள். மூன்று வரிகளின் இணைநிலை

நாம் ஏற்கனவே பிளானிமெட்ரியில் இணையான கோடுகளைப் படித்திருக்கிறோம். இப்போது நாம் விண்வெளியில் இணையான கோடுகளை வரையறுத்து அதனுடன் தொடர்புடைய தேற்றங்களை நிரூபிக்க வேண்டும்.

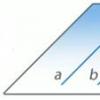
வரையறை: விண்வெளியில் உள்ள இரண்டு கோடுகள் ஒரே விமானத்தில் கிடக்கும் மற்றும் வெட்டாமல் இருந்தால் அவை இணையாக அழைக்கப்படுகின்றன (படம் 1.).

இணை கோடுகளின் பதவி: a || பி.

1. எந்த கோடுகள் இணையாக அழைக்கப்படுகின்றன?

2. கொடுக்கப்பட்ட இரண்டு இணை கோடுகளை வெட்டும் அனைத்து கோடுகளும் ஒரே விமானத்தில் உள்ளன என்பதை நிரூபிக்கவும்.

3. ஒரு கோடு கோடுகளை வெட்டுகிறது ஏபிமற்றும் கி.மு.வலது கோணங்களில். கோடுகள் இணையாக உள்ளதா? ஏபிமற்றும் கி.மு.?

4. வடிவியல். வகுப்புகள் 10-11: பொது கல்வி நிறுவனங்களின் மாணவர்களுக்கான பாடநூல் (அடிப்படை மற்றும் சிறப்பு நிலைகள்) / I. M. ஸ்மிர்னோவா, V. A. ஸ்மிர்னோவ். - 5வது பதிப்பு, சரி செய்யப்பட்டது மற்றும் விரிவாக்கப்பட்டது - எம்.: Mnemosyne, 2008. - 288 p. : உடம்பு சரியில்லை.

இரண்டு கோடுகள் வெட்டினால் அல்லது இணையாக இருந்தால், அவை ஒரே விமானத்தில் இருக்கும். இருப்பினும், விண்வெளியில், இரண்டு கோடுகள் ஒரே விமானத்தில் படாத வகையில் அமைந்திருக்கும், அதாவது, இந்த இரண்டு கோடுகளையும் கடந்து செல்லும் விமானம் இல்லை. அத்தகைய கோடுகள் வெட்டுவதில்லை அல்லது இணையாக இல்லை என்பது தெளிவாகிறது.

இரண்டு நேர் கோடுகளின் சாத்தியமான ஏற்பாட்டின் மூன்று நிகழ்வுகள் விண்வெளியில் கருதப்படுகின்றன. விண்வெளியில் இரண்டு நேர் கோடுகள்:

1. ஒரே விமானத்தில் படுத்து ஒரு பொதுவான புள்ளியைக் கொண்டிருங்கள்;

2. ஒரே விமானத்தில் படுத்து, பொதுவான புள்ளிகள் இல்லை;

ஒரே விமானத்தில் பொய் சொல்லாதீர்கள், எனவே, பொதுவான புள்ளிகள் இல்லை.

வரையறை: இரண்டு கோடுகள் ஒரு பொதுவான புள்ளியைக் கொண்டிருந்தால் அவை வெட்டும் என்று கூறப்படுகிறது.

வரையறை: இரண்டு கோடுகள் ஒரே விமானத்தில் அமைந்து, பொதுவான புள்ளிகள் இல்லாமல் அல்லது ஒத்துப்போகாமல் இருந்தால், அவை இணையாக அழைக்கப்படுகின்றன.

வரையறை: இரண்டு கோடுகள் வெட்டப்படாமலும், இணையாக இல்லாமலும் இருந்தால், அவை வளைவு எனப்படும் (ஒரே விமானத்தில் படுக்க வேண்டாம்).

பதவி:a · பி

நேர்கோடுகளை கடப்பதற்கான அடையாளம்

தேற்றம்: இரண்டு கோடுகளில் ஒன்று ஒரு விமானத்தில் அமைந்திருந்தால், மற்றொன்று இந்த விமானத்தை முதல் வரியைச் சேராத ஒரு புள்ளியில் வெட்டினால், இந்த கோடுகள் வெட்டுகின்றன.

கொடுக்கப்பட்டது: ; ; .

நிரூபிக்க:a · பி

ஆதாரம்: (முரணாக)

நாம் நிரூபிக்க விரும்புவதற்கு நேர்மாறாக, அதாவது, இந்த கோடுகள் வெட்டுகின்றன அல்லது இணையாக உள்ளன என்று வைத்துக்கொள்வோம்: .

ஒரு விமானத்தை இரண்டு வெட்டும் அல்லது இணையான கோடுகள் மூலம் வரையலாம். .

தேற்றத்தின் நிபந்தனைகளின்படி.

அனுமானத்தின் மூலம்.

தேற்றத்தின் நிபந்தனைகளிலிருந்தும், அனுமானத்திலிருந்தும், இரண்டு விமானங்களும் “a” மற்றும் அதற்குச் சொந்தமில்லாத புள்ளி M ஐக் கடந்து செல்கின்றன அது சொந்தமானது அல்ல, எனவே, விமானங்கள் ஒத்துப்போகின்றன. .

அனுமானத்தின் மூலம்.

நிபந்தனையின்படி.

தேற்றத்தின் நிபந்தனையுடன் எங்களுக்கு ஒரு முரண்பாடு கிடைத்தது, எனவே, அனுமானம் உண்மையல்ல, ஆனால் நிரூபிக்க வேண்டியது உண்மை, அதாவது, கோடுகள் வெட்டுகின்றன: a · பி.

வெட்டும் கோடுகளுக்கு இடையிலான கோணம் ஒரு புள்ளியின் வழியாக செல்லும் இணையான கோடுகளுக்கு இடையிலான கோணம் என்பதை நினைவில் கொள்க. வேறு வார்த்தைகளில் கூறுவதானால், நேராக இருந்தால் எல் o மற்றும் எல் 1 கடந்துவிட்டன, பின்னர் நாம் வரியின் இணையான மொழிபெயர்ப்பைச் செய்ய வேண்டும் எல் o , அதனால் அது ஒரு நேர் கோட்டாக மாறும் எல் o ¢ உடன் வெட்டும் எல் 1, மற்றும் இடையே உள்ள கோணத்தை அளவிடவும் எல் o ¢ மற்றும் எல் 1 .

இரண்டு வளைந்த கோடுகள் ஒரே செங்குத்தாக பொதுவானவை. அதன் நீளம் கோடுகளுக்கு இடையிலான தூரம் என்று அழைக்கப்படுகிறது.

விண்வெளியில் உள்ள இரண்டு கோடுகளை அவற்றின் நியதிச் சமன்பாடுகளால் வரையறுக்கலாம்:

எல் o: = =, எல் 1: = = . (35)

பின்னர் நாம் உடனடியாக முடிவு செய்யலாம் ( அ 1 , அ 2 , அ 3) ½½ எல்ஓ, ( பி 1 , பி 2 , பி 3) ½½ எல் 1 , ஏ o ( எக்ஸ்ஓ, ஒய்ஓ, z o)Î எல்ஓ, ஏ 1 (எக்ஸ் 1 , ஒய் 1 , z 1) ஓ எல் 1 . ஒரு மேட்ரிக்ஸை உருவாக்குவோம்

எக்ஸ் 1 – எக்ஸ்ஓ ஒய் 1 – ஒய்ஓ z 1 –zஓ

ஏ = அ 1 அ 2 அ 3 ,

பி 1 பி 2 பி 3

மற்றும் D = det ஏ.

தேற்றம் 8.1.l மற்றும் p இடையே உள்ள கோணம் சூத்திரத்தால் கணக்கிடப்படுகிறது

cos a = = . (36)

2. நேராக எல்ஓ மற்றும் எல் 1 இனக்கலப்புÛ D ≠ 0.

3. நேராக எல் o மற்றும் எல் 1 வெட்டுகின்றனÛ D = 0 மற்றும் கோலினியர் அல்ல.

4. எல் o½½ எல் 1 தரவரிசை ஏ= 2 மற்றும் ½½.

5. எல் o = எல் 1 தரவரிசை ஏ = 1.

ஆதாரம். 1. நேர் கோடுகளுக்கு இடையில் ஒரு கோணம் எல் o மற்றும் எல் 1 அவற்றின் திசை திசையன்களுக்கு இடையே உள்ள கோணம் b க்கு சமமாக இருக்கலாம் அல்லது அதற்கு அருகில் இருக்கலாம். முதல் வழக்கில்

cos a = cos b = ,

மற்றும் இரண்டாவது வழக்கில்

cos a = – cos b =½ cos b½ = .

இந்த சூத்திரம் முதல் வழக்குக்கும் பொருந்தும். வரைதல் ஒரு நேர் கோட்டைக் காட்டவில்லை என்பதை நினைவில் கொள்க எல் o , மற்றும் அதற்கு இணையான கோடு எல் o ¢ .

2, 3. வெளிப்படையாக, நேராக எல் o மற்றும் எல் 1 அவற்றின் திசை திசையன்கள் கோலினியர் இல்லை என்றால் மட்டுமே இணையாக இருக்காது. இந்த வழக்கில், கோடுகள் ஒரே விமானத்தில் உள்ளன மற்றும் வெட்டுகின்றன - திசையன்கள் கோப்லனர் - அவற்றின் கலப்பு தயாரிப்பு பூஜ்ஜியத்திற்கு சமம்: = 0. மேலும் ஆயத்தொலைவுகளில், துல்லியத்தின் இந்த தயாரிப்பு D க்கு சமம்.

அதன்படி, D ≠ 0 என்றால், திசையன்கள் கோப்லனர் அல்ல, எனவே நேராக இருக்கும் எல் o மற்றும் எல் 1 ஒரே விமானத்தில் படுக்காதீர்கள் Þ அவை வெட்டுகின்றன.

4, 5. என்றால் எல் o½½ எல் 1 அல்லது எல் o = எல் 1, பின்னர் ½½. ஆனால் முதல் வழக்கில், திசையன் கோலினியர் அல்ல, எனவே மேட்ரிக்ஸில் முதல் வரிசை ஏஇரண்டாவது மற்றும் மூன்றாவது வரிகளுக்கு ஏற்றதாக இல்லை. எனவே தரவரிசை ஏ = 2.

இரண்டாவது வழக்கில், மூன்று திசையன்களும் ஒன்றோடொன்று இணைக்கப்பட்டுள்ளன, எனவே, அனைத்து வரிசைகளும்

அணியில் ஏவிகிதாசார. எனவே தரவரிசை ஏ = 1.

மற்றும் நேர்மாறாக இருந்தால் || , பின்னர் நேராக எல் o மற்றும் எல் 1 இணை அல்லது தற்செயல்; இந்த வழக்கில், மேட்ரிக்ஸின் இரண்டாவது மற்றும் மூன்றாவது வரிசைகள் ஏவிகிதாசார. அதே நேரத்தில், தரவரிசை என்றால் ஏ= 2, பின்னர் மேட்ரிக்ஸின் முதல் வரிசை இரண்டாவது மற்றும் மூன்றாவது விகிதாச்சாரத்தில் இல்லை, அதாவது திசையன் கோலினியர் அல்லாதது மற்றும் Û எல் o || எல் 1 . தரவரிசை என்றால் ஏ= 1, பின்னர் மேட்ரிக்ஸில் உள்ள அனைத்து வரிசைகளும் ஏவிகிதாசாரமாக உள்ளன, அதாவது மூன்று திசையன்களும் ஒன்றோடொன்று இணையாக உள்ளன Û எல் o = எல் 1 .

தேற்றம் 9.இரண்டு நேர் கோடுகள் lஓ மற்றும் எல் 1 விண்வெளியில் அவற்றின் நியதிச் சமன்பாடுகளால் வழங்கப்படுகிறது (35). பிறகு

1. எல் என்றால் o½½ எல் 1 , பின்னர் l இடையே உள்ள தூரம்ஓ மற்றும் எல் 1 சூத்திரத்தால் கண்டறியப்படுகிறது

ம = , (37)

2. எல் என்றால்ஓ மற்றும் எல் 1 குறுக்கு, பின்னர் அவற்றுக்கிடையேயான தூரம் சூத்திரத்தால் கண்டறியப்படுகிறது

ம = . (38)

ஆதாரம். 1. விடுங்கள் எல் o½½ எல் 1 . புள்ளியில் இருந்து திசையன் வரைவோம் ஏ o , மற்றும் திசையன்கள் மீது மற்றும் நாம் ஒரு இணையான வரைபடத்தை உருவாக்குவோம். பின்னர் அதன் உயரம் மஇடையே உள்ள தூரம் இருக்கும் எல் o மற்றும் எல் 1 . இந்த இணையான வரைபடத்தின் பரப்பளவு: எஸ்=½ ´½, மற்றும் அடிப்படை ½ ½ ஆகும். அதனால் தான்

ம = எஸ்/½ ½ = (37).

2. விடுங்கள் எல் o மற்றும் எல் 1 கடந்தது. ஒரு நேர்கோடு வழியாக வரைவோம் எல் o விமானம் p o ½½ எல் 1, மற்றும் நேர் கோடு வழியாக எல் 1 விமானம் p 1 ½½ வரையவும் எல்ஓ.

பின்னர் பொதுவான செங்குத்தாக எல் o மற்றும் எல் 1 என்பது p o மற்றும் p 1 க்கு பொதுவான செங்குத்தாக இருக்கும். திசையன்கள் மற்றும் புள்ளியில் இருந்து வரைவோம் ஏ o மற்றும் வெக்டார்களில், மற்றும் ஒரு இணையான குழாய் கட்டமைக்க. பின்னர் அதன் கீழ் தளம் p o விமானத்திலும், அதன் மேல் தளம் p 1 விமானத்திலும் உள்ளது. எனவே, parallelepiped உயரம் p o மற்றும் p 1 க்கு பொதுவான செங்குத்தாக இருக்கும், மேலும் அதன் மதிப்பு மஇடையே உள்ள தூரம் இருக்கும் எல் o மற்றும் எல் 1 . இணையான குழாய்களின் அளவு ½ ½, மற்றும் அடித்தளத்தின் பரப்பளவு ½´½ Þ

ம= வி/எஸ்அடிப்படை = (38).

விளைவு. புள்ளி A இலிருந்து தூரம் 1 (எக்ஸ் 1 , ஒய் 1 , z 1) நேர் கோட்டிற்கு l, சமன்பாடு மூலம் கொடுக்கப்பட்டது

சூத்திரத்தால் கணக்கிடப்படுகிறது (37).

சிக்கலைத் தீர்ப்பதற்கான எடுத்துக்காட்டுகள்.

1. செங்குத்துகளின் ஆயத்தொலைவுகள் கொடுக்கப்பட்ட A(1,– 6), பி(–3, 0), சி(6, 9) முக்கோணம் ஏபிசி. ஒரு முக்கோணத்தைச் சுற்றி ஒரு வட்டத்திற்கு ஒரு சமன்பாட்டை எழுதுங்கள்.

தீர்வு. ஒரு வட்டத்தின் சமன்பாட்டை உருவாக்க, அதன் ஆரத்தை நாம் அறிந்து கொள்ள வேண்டும் ஆர்மற்றும் மைய ஒருங்கிணைப்புகள் பற்றி(அ, பி) பின்னர் சமன்பாடு இதுபோல் தெரிகிறது:

(எக்ஸ்–அ) 2 +(ஒய்–பி) 2 = ஆர் 2 .

ஒரு முக்கோணத்தைச் சுற்றி வளைக்கப்பட்ட ஒரு வட்டத்தின் மையம் இந்த முக்கோணத்தின் பக்கங்களுக்கு செங்குத்தாக இருபக்கங்களின் குறுக்குவெட்டில் உள்ளது. நடுப்புள்ளிகளின் ஆயங்களை கண்டறிதல் எம் 1 (எக்ஸ் 1 , ஒய் 1), மற்றும் எம் 3 (எக்ஸ் 3 , ஒய் 3) பக்கங்கள் கி.மு.மற்றும் ஏபிமுறையே:

x 1 = = =, ஒய் 1 = = = , எம் 1 .

அதேபோல் எம் 3 (–1,–3).

விடுங்கள் எல் 3 - நேர்கோடு, இது செங்குத்தாக இருசமமாக உள்ளது ஏபி, ஏ எல் 1 முதல் கி.மு.. பின்னர் = (– 4, 6) ^ எல் 3 மற்றும் எல் 3 கடந்து செல்கிறது எம் 3. எனவே அதன் சமன்பாடு:

– 4(எக்ஸ்+1) + 6(ஒய்+3) = 0.

அதேபோல் = (9, 9)^ எல் 3. எனவே சமன்பாடு எல் 1:

9(எக்ஸ்-) + 9(ஒய் -) = 0

எக்ஸ் + ஒய் – 6 = 0.

எங்களிடம் உள்ளது பற்றி =எல் 1 ஐ எல் 3. எனவே, ஒரு புள்ளியின் ஆயங்களைக் கண்டறிய பற்றிசமன்பாடுகளை ஒன்றாக தீர்க்க வேண்டியது அவசியம் எல் 1 மற்றும் எல் 3:

எக்ஸ் + ஒய் – 6 = 0 ,

– 4எக்ஸ் + 6ஒய் +14 = 0.

முதல் சமன்பாட்டை இரண்டாவது சமன்பாட்டுடன் 4 ஆல் பெருக்குவோம்:

எக்ஸ் + ஒய் – 6 = 0,

10ஒய் – 10 = 0.

இங்கிருந்து ஒய் = 1, எக்ஸ் = 5, ஓ(5, 1).

இருந்து தூரத்திற்கு ஆரம் சமம் பற்றிமுக்கோணத்தின் எந்த முனைகளிலும். நாங்கள் கண்டுபிடிக்கிறோம்:

ஆர் =½½= = .

எனவே ஒரு வட்டத்தின் சமன்பாடு:

(எக்ஸ் – 5) 2 + (ஒய்–1) 2 = 65.

2. வலது முக்கோண ABC யில், கால்களில் ஒன்றின் சமன்பாடு அறியப்படுகிறது 3எக்ஸ் – 2ஒய் + 5 = 0, உச்சி ஆயத்தொகுப்புகள் சி(–5,–5) மற்றும் நடுத்தர O இன் ஆயத்தொலைவுகள்(– 3/2,–3)ஹைப்போடென்யூஸ் ஏபி. ஒருங்கிணைப்புகளைக் கண்டறியவும்

செங்குத்துகள் A, B மற்றும் புள்ளி E இன் ஆயத்தொலைவுகள், BC பக்கத்துடன் தொடர்புடைய O க்கு சமச்சீர். ஏபிசி முக்கோணத்தின் இடைநிலைகளின் வெட்டுப்புள்ளியின் ஆயத்தொலைவுகளைக் கண்டறியவும் .

தீர்வு.யாருடைய சமன்பாடு நமக்கு கொடுக்கப்பட்டதோ அந்த கால் இருக்கட்டும் NE. இது வடிவத்தின் பொதுவான சமன்பாட்டால் வழங்கப்படுகிறது

கோடாரி + மூலம் + c = 0.

இந்த சமன்பாட்டில் வடிவியல் பொருள்

குணகங்கள் அமற்றும் பிசாதாரண வெக்டரின் ஆயத்தொலைவுகள் ( அ, பி) எனவே (3,-2)^ சூரியன்.

செங்குத்து சமன்பாட்டை உருவாக்குவோம் எல் = ஓ.டி.பக்கத்திற்கு NEமற்றும் புள்ளியின் ஆயங்களைக் கண்டறியவும் டி. திசையன் இணையாக இருக்கும் ஓ.டி., அதாவது இது இந்த வரியின் திசை திசையன் ஆகும். கூடுதலாக, புள்ளியின் ஆயங்களை நாங்கள் அறிவோம் பற்றிஇந்த நேர்கோட்டில். ஒரு அளவுரு சமன்பாட்டை உருவாக்குதல் எல்:

எக்ஸ் = – + 3டி, (*)

ஒய் = – 3 - 2டி .

எங்களிடம் உள்ளது டி = எல்நான் கி.மு.. எனவே, இந்த புள்ளியின் ஆயங்களை கண்டுபிடிக்க, நாம் சமன்பாடுகளை கூட்டாக தீர்க்க வேண்டும் எல்மற்றும் கி.மு.. மாற்றுவோம் எக்ஸ்மற்றும் ஒய் Eq இலிருந்து எல்சமன்பாட்டிற்குள் கி.மு.:

3(– + 3டி) –2(–3 -2டி)+5 = 0,

– + 9டி +6 +4டி+5 = 0,

13டி = –, டி டி= – .

நாங்கள் கண்டுபிடித்ததை மாற்றவும் டிசமன்பாட்டிற்குள் எல்மற்றும் புள்ளியின் ஆயங்களைக் கண்டறியவும் டி(–3,–2). ஆயத்தொலைவுகளைக் கண்டறிய ஈஒரு நேர் கோட்டின் அளவுரு சமன்பாட்டின் இயற்பியல் பொருளை நினைவில் கொள்வோம்: இது நேர்கோட்டு மற்றும் சீரான இயக்கத்தைக் குறிப்பிடுகிறது. எங்கள் விஷயத்தில், ஆரம்ப புள்ளி பற்றி OEபிரிவை விட இரண்டு மடங்கு நீளம் OD. காலத்தில் என்றால் டி டி= - நாங்கள் வெகுதூரம் வந்துவிட்டோம் பற்றிமுன் டி, பின்னர் இருந்து பாதை பற்றிமுன் ஈகாலத்தை கடந்து செல்வோம் டி ஈ= 2டி டி= –1. இந்த மதிப்பை (*) க்கு மாற்றுவது, நாம் கண்டுபிடிக்கிறோம் ஈ(– 4,5;–1).

புள்ளி டிஒரு பகுதியை பிரிக்கிறது கி.மு.பாதியில். அதனால் தான்

x D =, ஒய் டி = .

இங்கிருந்து நாம் கண்டுபிடிக்கிறோம்

x பி= 2xD– x சி= –1, ஒய் பி = 2ஒய் டி – ஒய் சி =1, பி(–1, 1).

அதேபோல், என்ற உண்மையைப் பயன்படுத்தி பற்றி- நடுத்தர ஏபி, புள்ளியின் ஆயங்களைக் கண்டறியவும் ஏ(-2,-7). இந்த சிக்கலை தீர்க்க மற்றொரு வழி உள்ளது: Δ ஐ முடிக்கவும் ஏபிசிஒரு இணையான வரைபடத்திற்கு.

இது சம்பந்தமாக ஒரு பகுதியைப் பிரிப்பதற்கான பொதுவான சூத்திரங்கள் இப்படி இருக்கும்:

x C =, ஒய் டி = ,

புள்ளி என்றால் உடன்ஒரு பகுதியை பிரிக்கிறது ஏபி l 1:l 2 என்ற விகிதத்தில், அதாவது. ½ ஏ.சி.½:½ கி.மு.½=l 1:l 2.

இடைநிலைகளின் வெட்டுப்புள்ளியானது, உச்சியில் இருந்து எண்ணி 2:1 என்ற விகிதத்தில் இடைநிலையை பிரிக்கிறது என்பது அறியப்படுகிறது. எங்கள் விஷயத்தில் ஆர்பிரிக்கிறது CO 2:1 என்ற விகிதத்தில். அதனால் தான்

x பி = = = – ,

ஒய் பி = = = – .

பதில்:ஏ(–2,–7), பி(–1, 1), பி.

3. செங்குத்துகளின் ஆயத்தொலைவுகள் கொடுக்கப்பட்ட A(– 4,–2), பி(9, 7), சி(2,– 4)முக்கோணம் ஏபிசி. AD என்ற இருசமயத்தின் பொதுவான சமன்பாட்டை உருவாக்கி புள்ளி D இன் ஆயத்தொலைவுகளைக் கண்டறியவும்.

தீர்வு. தொடக்கக் கணிதத்தின் போக்கிலிருந்து அது அறியப்படுகிறது = . நாங்கள் கணக்கிடுகிறோம்

(13, 9), (6,–2);

½½= = 5, ½½= = 2.

x D = = = 4,

ஒய் டி = = = – , டி(4,–).

புள்ளிகள் வழியாக செல்லும் ஒரு நேர் கோட்டின் சமன்பாட்டை நாங்கள் உருவாக்குகிறோம் ஏமற்றும் டி. அவளுக்கு, திசையன் ஒரு வழிகாட்டி. ஆனால் நாம் எந்த கோலினியர் வெக்டரையும் வழிகாட்டியாக எடுத்துக் கொள்ளலாம். எடுத்துக்காட்டாக, = , (7, 1) எடுக்க வசதியாக இருக்கும். பிறகு சமன்பாடு

கி.பி: = ஒய்+ 2 Û எக்ஸ் – 7ஒய்– 10 = 0.

பதில்:டி(4,–), கி.பி: எக்ஸ் – 7ஒய்– 10 = 0.

4. இரண்டு இடைநிலைகளின் சமன்பாடுகள் கொடுக்கப்பட்டால் x – ஒய்– 3 = 0, 5எக்ஸ் + 4ஒய்– 9 = 0 முக்கோணம் ABC மற்றும் உச்சி A இன் ஆயத்தொலைவுகள்(– 1, 2). மூன்றாவது இடைநிலைக்கு ஒரு சமன்பாட்டை எழுதுங்கள்.

தீர்வு.முதலில் நாம் புள்ளி என்பதை உறுதி செய்கிறோம் ஏஇந்த இடைநிலைகளுக்கு சொந்தமானது அல்ல. ஒரு முக்கோணத்தின் இடைநிலைகள் ஒரு புள்ளியில் வெட்டுகின்றன எம். எனவே அவை கடந்து செல்லும் கோடுகளின் தொகுப்பில் சேர்க்கப்பட்டுள்ளன எம். இந்த கற்றைக்கு ஒரு சமன்பாட்டை உருவாக்குவோம்:

l( எக்ஸ் – ஒய்– 3) + மீ(5 எக்ஸ் + 4ஒய்– 9) = 0.

குணகங்கள் l மற்றும் m ஆகியவை விகிதாச்சாரத்தில் தீர்மானிக்கப்படுகின்றன; எனவே, m = 1 (m = 0 எனில், பீம் சமன்பாடு முதல் இடைநிலையை மட்டுமே குறிப்பிடுகிறது, மேலும் விரும்பிய நேர்கோடு அதனுடன் ஒத்துப்போவதில்லை) என்று நாம் கருதலாம். பீம் சமன்பாட்டைப் பெறுகிறோம்:

(எல் + 5) எக்ஸ்+ (–எல் + 4) ஒய்– 3லி – 9 = 0.

இந்த பீமில் இருந்து நாம் புள்ளி வழியாக செல்லும் ஒரு நேர் கோட்டை தேர்ந்தெடுக்க வேண்டும் ஏ(- 12) பீம் சமன்பாட்டில் அதன் ஆயங்களை மாற்றுவோம்:

– (l + 5) + 2(–l + 4) – 3l – 9 = 0,

– 6l – 6 = 0, l = –1.

கற்றை சமன்பாட்டில் l இன் கண்டுபிடிக்கப்பட்ட மதிப்பை மாற்றி, விரும்பிய இடைநிலை சமன்பாட்டைப் பெறுகிறோம்:

4எக்ஸ் + 5ஒய்– 6 = 0.

பதில்: 4எக்ஸ் + 5ஒய்– 6 = 0.

5. முக்கோண பிரமிடு SABC இன் முனைகளின் ஆயத்தொலைவுகள் கொடுக்கப்பட்டுள்ளன: ஏ(–3, 7, 1), பி(–1, 9, 2), சி(–3, 6, 6) எஸ்(6,–5,–2). அடிப்படை விமானமான ஏபிசியின் சமன்பாட்டையும் உயரம் எஸ்டியின் சமன்பாட்டையும் எழுதுங்கள். புள்ளி D மற்றும் புள்ளி S இன் ஆயங்களைக் கண்டறியவும்¢ , அடித்தளத்தின் விமானத்துடன் தொடர்புடைய சமச்சீர் எஸ்.

தீர்வு.அடிப்படை p = விமானத்திற்கு இணையான இரண்டு திசையன்களின் ஆயத்தொலைவுகளைக் கண்டுபிடிப்போம் ஏபிசி:

= (2, 1, 1), = (0,–1, 5).

கொடுக்கப்பட்ட புள்ளியின் வழியாக செல்லும் விமானத்தின் சமன்பாடு ஏ(எக்ஸ்ஓ, ஒய்ஓ, z o) இரண்டு கோலினியர் அல்லாத திசையன்களுக்கு இணையாக ( அ 1 ,அ 2 , அ 3), (பி 1 ,பி 2 , பி 3) வடிவம் உள்ளது

எக்ஸ் – எக்ஸ்ஓ ஒய் – ஒய்ஓ z – zஓ

அ 1 அ 2 அ 3 = 0.

பி 1 பி 2 பி 3

இந்த சமன்பாட்டில் எங்கள் தரவை மாற்றுகிறோம்:

எக்ஸ் + 3 ஒய் – 7 z – 1

2 2 1 = 0.

0 –1 5

நாங்கள் தீர்மானிப்பதை விரிவுபடுத்துகிறோம்:

விமானத்தின் சமன்பாட்டிலிருந்து திசையன் (11,–10,–2) விமானத்தின் சாதாரண திசையன் என்பதைக் காண்கிறோம். அதே திசையன் நேர்கோட்டிற்கான வழிகாட்டியாக இருக்கும் ம = எஸ்டி. கொடுக்கப்பட்ட புள்ளியின் வழியாக செல்லும் கோட்டின் அளவுரு சமன்பாடு ஏ(எக்ஸ்ஓ, ஒய்ஓ, z o) திசை வெக்டருடன் ( அ 1 ,அ 2 , அ 3) வடிவம் உள்ளது

எக்ஸ் = எக்ஸ் o + அ 1 டி ,

ஒய் = ஒய் o + அ 2 டி ,

z = z o + அ 3 டி .

எங்கள் விஷயத்தில் நாம் சமன்பாட்டைப் பெறுகிறோம்:

எக்ஸ் = 6 + 11டி ,

ம: ஒய் = –5 – 10டி , (*)

z = –2 – 2டி .

செங்குத்தான அடிப்பகுதியைக் கண்டுபிடிப்போம். இது விமானம் p உடன் கோட்டின் வெட்டும் புள்ளியாகும். இதைச் செய்ய, நாம் சமன்பாடுகளையும் p ஐயும் ஒன்றாக தீர்க்க வேண்டும். சமன்பாட்டில் இருந்து மாற்றுதல் எல்π சமன்பாட்டிற்குள்:

11(6 + 11டி) – 10(–5 – 10 டி) – 2(–2 – 2டி) + 105 = 0,

66 + 121 டி + 50 + 100 டி + 4 + 4 டி + 105 = 0,

225 ஒய் = –225, டி = –1.

கண்டறியப்பட்டது டிசமன்பாட்டில் மாற்று எல்மற்றும் ஒருங்கிணைப்புகளைக் கண்டறியவும் டி(–5, 5, 0).

ஒரு நேர்கோட்டின் அளவுரு சமன்பாட்டின் இயற்பியல் பொருளை நினைவுபடுத்துவோம்: இது நேர்கோட்டு மற்றும் சீரான இயக்கத்தைக் குறிப்பிடுகிறது. எங்கள் விஷயத்தில், ஆரம்ப புள்ளி எஸ், திசைவேகம் திசையன் ஆகும். கோட்டு பகுதி எஸ்.எஸ்¢ பிரிவை விட இரண்டு மடங்கு நீளம் எஸ்டிஅதை முடிக்க இரண்டு மடங்கு நேரம் எடுக்கும். காலத்தில் என்றால் டி டி= – 1 நாங்கள் சென்றுள்ளோம் எஸ்முன் டி, பின்னர் இருந்து பாதை எஸ்முன் எஸ்¢ காலத்தை கடந்து செல்வோம் டி¢= 2 டி டி= –2. இந்த மதிப்பை (*) க்கு மாற்றுவது, நாம் கண்டுபிடிக்கிறோம் எஸ்¢(–16, 15; 2).

பதில்:ஏபிசி: 11எக்ஸ் – 10ஒய்– 2z +105 = 0, டி(–5, 5, 0), எஸ்¢(–16, 15; 2),

எக்ஸ் = 6 + 11டி ,

எஸ்டி: ஒய் = –5 – 10டி ,

z = –2 – 2டி .

6. p இன் நேர் கோட்டின் சமன்பாடுகள் கொடுக்கப்பட்டுள்ளன:

l மற்றும் p குறுக்கிடுவதை உறுதிசெய்து, l இன் திட்டத்திற்கான சமன்பாட்டை உருவாக்கவும்¢ விமானத்திற்கு நேர் கோடு l. l மற்றும் p இடையே உள்ள கோணத்தைக் கண்டறியவும் .

தீர்வு. ஒரு கோட்டின் சமன்பாட்டிலிருந்து அதன் திசை திசையன்: (1,–1, 2) மற்றும் இந்த வரியில் ஒரு புள்ளி: ஏ(6, 0, 2) , மற்றும் விமானத்தின் சமன்பாட்டிலிருந்து - விமானத்திற்கு சாதாரண திசையன்:

(5,–2, 4). வெளிப்படையாக, என்றால் எல்½½ p அல்லது, பின்னர் ^ அதாவது. · = 0. சரிபார்ப்போம்:

· = 5 1 – 2 (–1) + 4 2 = 15 ¹ 0.

பொருள் எல்π ஐ வெட்டுகிறது. இடையே கோணம் எல்மற்றும் p ஆகியவை சூத்திரத்தால் கண்டறியப்படுகின்றன:

பாவம் அ = ;

|| = = , || = = = 3 .

பாவம் அ = = .

விடுங்கள் ஏ o - புள்ளி கணிப்பு ஏஒரு விமானத்தில், மற்றும் பி = எல்நான் π . பிறகு எல்¢= ஏஓ பிஒரு நேர்கோட்டின் திட்டமாகும். முதலில் புள்ளியின் ஆயங்களை கண்டுபிடிப்போம் பி. இதைச் செய்ய, நேர் கோட்டின் சமன்பாட்டை மீண்டும் எழுதுகிறோம் எல்அளவுரு வடிவத்தில்:

எக்ஸ் = 6 + டி,

எல்: ஒய் = – டி,

z = 2 + 2டி,

மற்றும் அதை விமானத்தின் சமன்பாட்டுடன் ஒன்றாக தீர்க்கவும் π . சமன்பாட்டில் இருந்து மாற்றுதல் எல்சமன்பாட்டிற்குள் π :

5(6 + டி) – 2(– டி) + 4(2 + 2டி) + 7 = 0,

30 + 5டி + 2டி + 8 + 8டி + 7 = 0,

15டி = – 45, டி = – 3.

இதை மாற்றுவது டிசமன்பாட்டிற்குள் எல்ஒருங்கிணைப்புகளைக் கண்டறியவும் பி(3, 3, 4). செங்குத்து சமன்பாட்டை உருவாக்குவோம் ம = ஏ.ஏ.ஓ. நேராக மதிசையன் ஒரு வழிகாட்டியாக செயல்படுகிறது. அதனால் தான் மசமன்பாடு மூலம் கொடுக்கப்பட்டது

எக்ஸ் = 6 + 5டி,

ம: ஒய் = –2 டி,

z = 2 + 4டி,

புள்ளியின் ஒருங்கிணைப்புகளைக் கண்டறிய π விமானத்தின் சமன்பாட்டுடன் அதைத் தீர்க்கிறோம் ஏ o:

5(6 + 5டி) – 2(–2டி) + 4(2 + 4டி) + 7 = 0,

30 + 25டி + 4டி + 8 + 16டி + 7 = 0,

45டி = – 45, டி = – 1.

இதை மாற்றுவோம் டிசமன்பாட்டிற்குள் மமற்றும் நாங்கள் கண்டுபிடிக்கிறோம் ஏ o (1, 2,–2). கோட்டின் திசை வெக்டரைக் கண்டறிதல் l": ஏஓ பி(2, 1,–2) மற்றும் அதன் சமன்பாட்டைப் பெறவும்:

.

7. விண்வெளியில் உள்ள நேர்கோடு l என்பது சமன்பாடுகளின் அமைப்பால் வழங்கப்படுகிறது

2எக்ஸ்+2ஒய்– z– 1=0,

4எக்ஸ்– 8ஒய்+ z – 5= 0,

மற்றும் புள்ளி A இன் ஆயங்கள் கொடுக்கப்பட்டுள்ளன(–5,6,1). புள்ளி B இன் ஆயத்தொலைவுகளைக் கண்டறியவும், நேர்கோடு l உடன் தொடர்புடைய A க்கு சமச்சீர்.

தீர்வு.விடுங்கள் பி- ஒரு புள்ளியில் இருந்து செங்குத்தாக கீழே விழுந்தது ஏநேரடியாக எல். முதலில் நாம் புள்ளியின் ஆயங்களை கண்டுபிடிப்போம் பி. இதைச் செய்ய, புள்ளியின் வழியாக செல்லும் p விமானத்திற்கான சமன்பாட்டை உருவாக்குவோம் ஏ p 1 மற்றும் p 2 விமானங்களுக்கு செங்குத்தாக. இந்த விமானங்களுக்கான சாதாரண திசையன்களைக் காண்கிறோம்: (2, 2,–1), (4,–8, 1). விமானம் p க்கு அவர்கள் வழிகாட்டியாக இருப்பார்கள். எனவே, இந்த விமானத்தின் சமன்பாடு:

எக்ஸ் + 5 ஒய் – 6 z – 1

2 2 –1 = 0.

4 –8 1

– 6(எக்ஸ் + 5) – 6(ஒய் – 6) –24(z – 1) = 0 .

அடைப்புக்குறிகளைத் திறப்பதற்கு முன், கண்டிப்பாக

முதலில், முழு சமன்பாட்டையும் - 6 ஆல் வகுக்கவும்:

எக்ஸ் + 5 + ஒய் – 6 + 4(z – 1) = 0,

x+ y+ 4z – 5 = 0.

இப்போது பி- விமானங்கள் p, p 1 மற்றும் p 2 வெட்டும் புள்ளி. அதன் ஒருங்கிணைப்புகளைக் கண்டறிய, இந்த விமானங்களின் சமன்பாடுகளால் உருவாக்கப்பட்ட ஒரு அமைப்பை நாம் தீர்க்க வேண்டும்:

எக்ஸ் + ஒய் + 4z – 5 = 0,

4எக்ஸ் – 8ஒய் + z – 5 = 0,

2எக்ஸ் + 2ஒய் – z – 1 = 0.

காஸ் முறையைப் பயன்படுத்தி அதைத் தீர்ப்பது, நாங்கள் காண்கிறோம் பி(1,0,1) அடுத்து, என்ற உண்மையைப் பயன்படுத்தி பி- நடுத்தர ஏபிபுள்ளியின் ஆயங்களை நாம் காண்கிறோம் பி(7,–6,1).

முற்றுப்புள்ளி பிமிக நெருக்கமான மற்றொரு வழியில் காணலாம் ஏஒரு நேர் கோட்டின் புள்ளி எல். இதைச் செய்ய, இந்த வரிக்கு ஒரு அளவுரு சமன்பாட்டை உருவாக்குவது அவசியம். இது எவ்வாறு செய்யப்படுகிறது, பணியைப் பார்க்கவும் 10 . மேலும் செயல்களுக்கு, பணியைப் பார்க்கவும் 8 .

8. INடி ஏபிசி முனைகளுடன் A(9, 5, 1), பி(–3, 8, 4), சி(9,–13,–8) உயரம் AD வரையப்பட்டது. புள்ளி D இன் ஆயத்தொலைவுகளைக் கண்டறியவும், AD வரியின் சமன்பாட்டை எழுதவும், h கணக்கிட=½ கி.பி½ மற்றும் h ஐ கணக்கிடுவதன் மூலம் சரிபார்க்கவும்எஸ் டி குறுக்கு தயாரிப்பு பயன்படுத்தி ஏபிசி.

தீர்வு.வெளிப்படையாக புள்ளி டிஇவ்வாறு காணலாம்: டி= π ஐ கி.மு., π என்பது புள்ளியின் வழியாக செல்லும் விமானம் ஏபக்கத்திற்கு செங்குத்தாக கி.மு.. இந்த விமானம் சாதாரண வெக்டராக செயல்படுகிறது. நாம் (12,–21,–12) கண்டுபிடிக்கிறோம். இந்த வெக்டரின் ஆயத்தொலைவுகள் 3 ஆல் முற்றிலும் வகுபடும். எனவே, p க்கு சாதாரண திசையன் என நாம் = , (4,–7,–4) என எடுத்துக் கொள்ளலாம். ஒரு புள்ளி வழியாக செல்லும் விமானத்தின் சமன்பாடு π ஏ o ( எக்ஸ்ஓ, ஒய்ஓ, z o) வெக்டருக்கு செங்குத்தாக ( அ, பி, c), வடிவம் உள்ளது:

அ(எக்ஸ் – எக்ஸ் o) + பி(ஒய் – ஒய் o) + c(z – z o) = 0.

எங்கள் விஷயத்தில்:

4(எக்ஸ் – 9) - 7(ஒய் – 5) - 4(z – 1) = 0,

4எக்ஸ் - 7ஒய் - 4z + 3 = 0,

ஒரு நேர்கோட்டின் சமன்பாட்டை உருவாக்குவோம் கி.மு.. அவளுக்கு, திசையன் ஒரு வழிகாட்டியாக இருக்கும்:

எக்ஸ் = –3 + 4டி,

கி.மு.: ஒய் = 8 – 7டி, (*)

z = 4 – 4டி,

ஏனெனில் டி= π ஐ கி.மு., ஒரு புள்ளியின் ஆயங்களைக் கண்டறிய டிசமன்பாடுகள் ஒன்றாக தீர்க்கப்பட வேண்டும் π மற்றும் கி.மு.. சமன்பாட்டில் இருந்து மாற்றுதல் கி.மு.π சமன்பாட்டிற்குள்:

4(–3 + 4டி) – 7(8 – 7டி) – 4(4 – 4டி) + 3 = 0,

–12 + 16 டி – 56 + 49டி – 16 + 16 டி + 3 = 0,

81டி = 81, டி = 1.

இதை மாற்றுவோம் டிஒரு கோட்டின் சமன்பாட்டில் கி.மு.மற்றும் நாங்கள் கண்டுபிடிக்கிறோம் டி(1, 1, 0). அடுத்து, புள்ளிகளின் ஆயங்களை அறிவது ஏமற்றும் டி, நாம் நேர்கோட்டின் சமன்பாட்டை உருவாக்குகிறோம் கி.பிசூத்திரத்தைப் பயன்படுத்தி புள்ளிகளுக்கு இடையிலான தூரத்தைக் கணக்கிடுகிறோம்:

நான் ஜே கே ஐ ஜே கே

´ = –12 3 3 = –27· – 4 1 1 = –27(– நான் + 4ஜே– 8கே) .

0 –18 –9 0 2 1

(கணக்கீடு செயல்பாட்டில், நாங்கள் தீர்மானிப்பவரின் சொத்தைப் பயன்படுத்தினோம்: ஒரு வரியின் உறுப்புகளின் பொதுவான காரணியை தீர்மானிப்பவரின் அடையாளத்திலிருந்து எடுக்கலாம்).

SΔ ஏபிசி= · 27 = .

மறுபுறம், S Δ ஏபிசி = | |· ம. இங்கிருந்து ம= கண்டுபிடிக்கிறோம்

அதனால் தான் ம= 9. இது முன்பு கிடைத்த பதிலுடன் பொருந்துகிறது.

முற்றுப்புள்ளி டிஅருகில் இருப்பதைக் காணலாம் ஏஒரு நேர் கோட்டின் புள்ளி கி.மு.வேறுபட்ட கால்குலஸ் முறைகளைப் பயன்படுத்துதல். விடுங்கள் எம்(டி) - ஒரு நேர் கோட்டின் தன்னிச்சையான புள்ளி கி.மு.; அதன் ஆயத்தொகுப்புகள் அமைப்பால் தீர்மானிக்கப்படுகின்றன (*):

எம்(–3 + 4டி, 8 – 7டி, 4 – 4டி).

ஒரு புள்ளியிலிருந்து சதுர தூரத்தைக் கண்டறிதல் ஏமுன் எம்(டி):

ம 2 (டி) = (9 + 3 – 4டி) 2 + (5 – 8 + 7டி) 2 + (1 – 4 + 4டி) 2

= (12 – 4டி) 2 + (–3 + 7டி) 2 + (–3 + 4டி) 2 =

144 – 96டி + 16டி 2 + 9 – 42டி + 49டி 2 + 9 – 24டி + 16டி 2 =

81டி 2 – 162டி + 162.

செயல்பாட்டின் சிறிய மதிப்பைக் கண்டுபிடிப்போம் ம 2 (டி) வழித்தோன்றலைப் பயன்படுத்துதல்:

ம 2 (டி) = 162டி – 162; ம 2 (டி) = 0 Þ டி = 1.

இந்த மதிப்பை மாற்றவும் டிஒரு கோட்டின் சமன்பாட்டில் கி.மு.மற்றும் நாம் அதை கண்டுபிடிக்க டி(1, 1, 0) அருகில் உள்ளது ஏஒரு வரியில் புள்ளி கி.மு..

9. பின்வரும் ஜோடி விமானங்களின் ஒப்பீட்டு நிலையை ஆராயவும்(வெட்டு, இணை, இணை). விமானங்கள் வெட்டினால், அவை இணையாக இருந்தால் அவற்றுக்கிடையேயான கோணத்தைக் கண்டறியவும் – அவர்களுக்கு இடையே உள்ள தூரம்.

A). p1:2 ஒய்+ z + 5 = 0, ப 2: 5 எக்ஸ் + 4ஒய்– 2z +11 = 0.

தீர்வு.விமானங்கள் p 1 மற்றும் p 2 அவற்றின் பொதுவான சமன்பாடுகளால் கொடுக்கப்பட்டால்

அ 1 எக்ஸ் + பி 1 ஒய் + c 1 z + ஈ 1 = 0, அ 2 எக்ஸ் + பி 2 ஒய் + c 2 z + ஈ 2 = 0,

ப 1 ½½ ப 2 Û = = ¹ ,

ப 1 = ப 2 Û = = = .

எங்கள் விஷயத்தில், ¹ ¹, எனவே விமானங்கள் இணையாக இல்லை மற்றும் ஒத்துப்போவதில்லை. இதன் பொருள் அவை வெட்டுகின்றன. விமானங்களுக்கு இடையிலான கோணம் சூத்திரத்தால் கணக்கிடப்படுகிறது

cos அ = ,

இந்த விமானங்களுக்கான சாதாரண திசையன்கள் எங்கே மற்றும் அவை. எங்கள் விஷயத்தில்

(0, 2, 1), (5, 4,–2), · = 0·5 + 2· 4 + 1·(–2);

|| = = , || = = 3 .

எனவே காஸ் அ = = .

பதில்: a = ஆர்க்கோஸ்.

b)ப1: எக்ஸ் – ஒய்+ 2z + 8 = 0,

ப 2:2 எக்ஸ் – ஒய்+ 4z –12 = 0.

தீர்வு.இணையானதா அல்லது தற்செயலானதா எனச் சரிபார்க்கிறது:

இதன் பொருள் p 1 ½½ p 2 ஆனால் p 1 ¹ p 2 . புள்ளியிலிருந்து தூரம் ஏ(எக்ஸ், ஒய், z) சமன்பாட்டால் குறிப்பிடப்பட்ட விமானம் சூத்திரத்தால் கண்டறியப்படுகிறது

ம = .

ஒரு புள்ளியைத் தேர்ந்தெடுப்போம் ஏஒப் 1 . இதைச் செய்ய, p 1 சமன்பாட்டை பூர்த்தி செய்யும் மூன்று ஆயங்களை நீங்கள் தேர்ந்தெடுக்க வேண்டும். எங்கள் விஷயத்தில், எளிமையான விஷயம்: ஏ o (0, 8, 0). இருந்து தூரம் ஏ o முதல் ப 2 வரை மற்றும் ப 1 மற்றும் ப 2 இடையே இருக்கும் தூரம்:

ம = = .

10. விமானத்தின் சமன்பாட்டை உருவாக்கவும்ப, இது விமானங்களுக்கு இடையே உள்ள இருமுனைக் கோணங்களில் ஒன்றைப் பிரிக்கிறது

p1:2 எக்ஸ்– ஒய்+ 2= 0, ப 2: 5 எக்ஸ்+ 4ஒய்– 2z–14 = 0,

இதில் இந்த புள்ளி ஏ உள்ளது(0, 3,–2). l நேர் கோட்டின் அளவுரு சமன்பாட்டை உருவாக்கவும் = ப 1 ஐ ப 2 ;

தீர்வு.புள்ளியானது இருஹெட்ரல் கோணத்தை பிளவுபடுத்தும் p விமானத்தில் இருந்தால், தூரங்கள் ம 1 மற்றும் ம 2 இந்த புள்ளியில் இருந்து p 1 மற்றும் p 2 க்கு சமம்.

இந்த தூரங்களைக் கண்டுபிடித்து அவற்றை சமன் செய்கிறோம்:

ஒரே மாதிரியான அல்லது வெவ்வேறு அடையாளங்களுடன் தொகுதிகளை திறக்கலாம். எனவே, நாம் 2 பதில்களைப் பெறலாம், ஏனென்றால்... p 1 மற்றும் p 2 இரண்டு டைஹெட்ரல் கோணங்களை உருவாக்குகின்றன. ஆனால் நிபந்தனைக்கு புள்ளி அமைந்துள்ள கோணத்தை பிளவுபடுத்தும் விமானத்தின் சமன்பாட்டைக் கண்டறிய வேண்டும். ஏ. எனவே புள்ளியின் ஆயத்தொலைவுகள் எம்இந்த விமானங்களின் சமன்பாடுகளின் இடது பக்கங்களில் மாற்றும் போது ப 1 மற்றும் புள்ளியின் ஆயத்தொலைவுகளின் அதே அடையாளங்களைக் கொண்டிருக்க வேண்டும் ஏ. இந்த அறிகுறிகள் ப 1 மற்றும் "+" ப 2க்கு உள்ளதா என்பதைச் சரிபார்ப்பது எளிது. எனவே, முதல் தொகுதியை “–” அடையாளத்துடன் விரிவுபடுத்துகிறோம், இரண்டாவது “+” அடையாளத்துடன்:

3(-2எக்ஸ் + ஒய்- 2) = 5எக்ஸ்+ 4ஒய்– 2z–14,

ப:11 எக்ஸ் + ஒய் - 2z - 14 = 0.

நேர்கோட்டின் சமன்பாட்டை உருவாக்குவதற்காக எல், இந்த வரியின் திசை வெக்டரையும் அதில் உள்ள புள்ளியையும் நாம் கண்டுபிடிக்க வேண்டும்.

சமன்பாடுகள் p 1 மற்றும் p 2 இலிருந்து இந்த விமானங்களுக்கான சாதாரண திசையன்களின் ஆயத்தொலைவுகளைக் காணலாம்: (2,–1, 0), (5, 4,–2). நேரடி திசையன் எல்செங்குத்தாக மற்றும் திசையன் தயாரிப்பைப் பயன்படுத்தி இதைக் காணலாம் (வரையறையின்படி, = ´, பின்னர் ^ மற்றும் ^):

= ´ = 2 –1 0 = 2 நான் + 4ஜே+ 13கே .

ஒரு வரியில் ஒரு புள்ளியின் ஆயத்தொலைவுகளைக் கண்டறிய, சமன்பாடுகளின் அமைப்பிற்கு ஒரு குறிப்பிட்ட தீர்வைக் கண்டுபிடிக்க வேண்டும்.

இரண்டு சமன்பாடுகள் மற்றும் மூன்று அறியப்படாதவை இருப்பதால், கணினியில் எண்ணற்ற தீர்வுகள் உள்ளன. நாம் செய்ய வேண்டியதெல்லாம் ஒன்றைத் தேர்ந்தெடுப்பதுதான். வைப்பதே எளிதான வழி எக்ஸ்= 0 பின்னர் நாம் கண்டுபிடிக்கிறோம்

Þ z = – 3, .

ஒரு புள்ளியின் வழியாக செல்லும் கோட்டின் நியதிச் சமன்பாடு பி(எக்ஸ்ஓ, ஒய்ஓ, z o) வெக்டருக்கு இணையாக ( அ 1 , அ 2 , அ 3), வடிவம் உள்ளது:

எங்கள் விஷயத்தில் சமன்பாடு உள்ளது:

எல்: = = .

பதில்:ப: 11 எக்ஸ் + ஒய் – 2z = 0, எல்: = = .

11. விண்வெளியில் இரண்டு கோடுகளின் சமன்பாடுகள் கொடுக்கப்பட்டுள்ளன:

எக்ஸ் = –1 – டி, எக்ஸ் = –3 + 2டி¢,

எல் 1: ஒய் = 6 + 2 டி, எல் 2: ஒய் = –2 – 3டி¢,

z = 5 + 2டி, z = 3 – 2டி¢.

இந்த கோடுகள் வெட்டுகின்றன மற்றும் அவற்றின் பொதுவான செங்குத்தாக ஒரு சமன்பாட்டை உருவாக்குகின்றன என்பதை நிரூபிக்கவும்.

தீர்வு.கோடுகளின் சமன்பாடுகளிலிருந்து அவற்றின் திசை திசையன்களின் ஆயத்தொலைவுகளை நாம் காண்கிறோம்: (–1, 2, 2), (2,–3,–2) மற்றும் புள்ளிகள் l 1, அதாவது இது பொதுவான செங்குத்தாக திசை திசையன் ஆகும். இந்த வரிகள். அதன் ஒருங்கிணைப்புகளை நாங்கள் ஏற்கனவே கண்டறிந்துள்ளோம்: (2, 2,–1). பொருட்டு

ஒரு சமன்பாட்டை எழுதுங்கள் மஇந்த வரியில் ஒரு புள்ளியின் ஆயங்களை நாம் கண்டுபிடிக்க வேண்டும். இதைச் செய்ய, விமானம் π கடந்து செல்லும் சமன்பாட்டை உருவாக்குவோம் எல் 1 மற்றும் ம. அவளைப் பொறுத்தவரை, திசையன்கள் வழிகாட்டிகளாக இருக்கும், மற்றும் ஏÎp.

எக்ஸ் – 1 ஒய் – 2 z – 1

– 6(எக்ஸ் – 1) + 3(ஒய் – 2) – 6(z – 1) = 0.

– 2(எக்ஸ் – 1) + (ஒய் – 2) – 2(z – 1) = 0.

ப: –2 எக்ஸ் + ஒய் – 2z + 2 = 0.

வெட்டும் புள்ளியைக் கண்டறிதல் எல் 2 மற்றும் π. இதைச் செய்ய, சமன்பாட்டிலிருந்து எல் 2 சமன்பாட்டில் π ஐ மாற்றுகிறோம்:

–2(–3 + 2டி¢) –2 + 3 டி¢ – 2(3 – 2 டி¢) + 2 = 0,

6 – 4டி¢ – 2 – 3 டி¢ – 6 – 4 டி¢ + 2 = 0,

–7டி¢= 0, டி¢= 0.

நாங்கள் கண்டுபிடித்ததை மாற்றவும் டி¢ இல்

உங்கள் தனியுரிமையை பராமரிப்பது எங்களுக்கு முக்கியம். இந்த காரணத்திற்காக, உங்கள் தகவலை நாங்கள் எவ்வாறு பயன்படுத்துகிறோம் மற்றும் சேமிப்போம் என்பதை விவரிக்கும் தனியுரிமைக் கொள்கையை நாங்கள் உருவாக்கியுள்ளோம். எங்கள் தனியுரிமை நடைமுறைகளை மதிப்பாய்வு செய்து, ஏதேனும் கேள்விகள் இருந்தால் எங்களுக்குத் தெரியப்படுத்தவும்.

தனிப்பட்ட தகவல்களை சேகரித்தல் மற்றும் பயன்படுத்துதல்

தனிப்பட்ட தகவல் என்பது ஒரு குறிப்பிட்ட நபரை அடையாளம் காண அல்லது தொடர்பு கொள்ள பயன்படுத்தப்படும் தரவைக் குறிக்கிறது.

நீங்கள் எங்களைத் தொடர்பு கொள்ளும்போது எந்த நேரத்திலும் உங்கள் தனிப்பட்ட தகவலை வழங்குமாறு கேட்கப்படலாம்.

நாங்கள் சேகரிக்கக்கூடிய தனிப்பட்ட தகவல்களின் சில எடுத்துக்காட்டுகள் மற்றும் அத்தகைய தகவலை நாங்கள் எவ்வாறு பயன்படுத்தலாம்.

என்ன தனிப்பட்ட தகவல்களை நாங்கள் சேகரிக்கிறோம்:

• நீங்கள் தளத்தில் விண்ணப்பத்தை சமர்ப்பிக்கும் போது, ​​உங்கள் பெயர், தொலைபேசி எண், மின்னஞ்சல் முகவரி போன்ற பல்வேறு தகவல்களை நாங்கள் சேகரிக்கலாம்.

உங்கள் தனிப்பட்ட தகவலை நாங்கள் எவ்வாறு பயன்படுத்துகிறோம்:

• நாங்கள் சேகரிக்கும் தனிப்பட்ட தகவல்கள், தனித்துவமான சலுகைகள், விளம்பரங்கள் மற்றும் பிற நிகழ்வுகள் மற்றும் வரவிருக்கும் நிகழ்வுகளுடன் உங்களைத் தொடர்புகொள்ள அனுமதிக்கிறது.
• அவ்வப்போது, ​​முக்கியமான அறிவிப்புகள் மற்றும் தகவல்தொடர்புகளை அனுப்ப உங்கள் தனிப்பட்ட தகவலை நாங்கள் பயன்படுத்தலாம்.
• நாங்கள் வழங்கும் சேவைகளை மேம்படுத்துவதற்கும் எங்கள் சேவைகள் தொடர்பான பரிந்துரைகளை உங்களுக்கு வழங்குவதற்கும் தணிக்கைகள், தரவு பகுப்பாய்வு மற்றும் பல்வேறு ஆராய்ச்சி போன்ற உள் நோக்கங்களுக்காக தனிப்பட்ட தகவலைப் பயன்படுத்துவோம்.
• பரிசுக் குலுக்கல், போட்டி அல்லது அது போன்ற விளம்பரங்களில் நீங்கள் பங்கேற்றால், அத்தகைய திட்டங்களை நிர்வகிக்க நீங்கள் வழங்கும் தகவலை நாங்கள் பயன்படுத்தலாம்.

மூன்றாம் தரப்பினருக்கு தகவலை வெளிப்படுத்துதல்

உங்களிடமிருந்து பெறப்பட்ட தகவல்களை மூன்றாம் தரப்பினருக்கு நாங்கள் வெளியிட மாட்டோம்.

விதிவிலக்குகள்:

• தேவைப்பட்டால் - சட்டம், நீதித்துறை நடைமுறை, சட்ட நடவடிக்கைகளில், மற்றும்/அல்லது ரஷ்ய கூட்டமைப்பின் பிரதேசத்தில் உள்ள அரசாங்க அதிகாரிகளிடமிருந்து பொது கோரிக்கைகள் அல்லது கோரிக்கைகளின் அடிப்படையில் - உங்கள் தனிப்பட்ட தகவலை வெளிப்படுத்த. பாதுகாப்பு, சட்ட அமலாக்கம் அல்லது பிற பொது முக்கியத்துவம் வாய்ந்த நோக்கங்களுக்காக அத்தகைய வெளிப்படுத்தல் அவசியம் அல்லது பொருத்தமானது என்று நாங்கள் தீர்மானித்தால், உங்களைப் பற்றிய தகவலையும் நாங்கள் வெளியிடலாம்.
• மறுசீரமைப்பு, இணைப்பு அல்லது விற்பனையின் போது, ​​நாங்கள் சேகரிக்கும் தனிப்பட்ட தகவலை பொருந்தக்கூடிய மூன்றாம் தரப்பினருக்கு மாற்றலாம்.

தனிப்பட்ட தகவல்களின் பாதுகாப்பு

உங்கள் தனிப்பட்ட தகவல்களை இழப்பு, திருட்டு மற்றும் தவறாகப் பயன்படுத்துதல், அத்துடன் அங்கீகரிக்கப்படாத அணுகல், வெளிப்படுத்துதல், மாற்றம் செய்தல் மற்றும் அழித்தல் போன்றவற்றிலிருந்து பாதுகாப்பதற்கு - நிர்வாகம், தொழில்நுட்பம் மற்றும் உடல்நிலை உள்ளிட்ட முன்னெச்சரிக்கை நடவடிக்கைகளை மேற்கொள்கிறோம்.

நிறுவன அளவில் உங்கள் தனியுரிமைக்கு மதிப்பளித்தல்

உங்கள் தனிப்பட்ட தகவல் பாதுகாப்பானது என்பதை உறுதிப்படுத்த, நாங்கள் எங்கள் ஊழியர்களுக்கு தனியுரிமை மற்றும் பாதுகாப்பு தரங்களைத் தொடர்புகொண்டு தனியுரிமை நடைமுறைகளை கண்டிப்பாகச் செயல்படுத்துகிறோம்.

இந்த கட்டுரையில், முப்பரிமாண இடைவெளியில் ஒரு நேர் கோட்டின் கருத்தைப் புரிந்துகொள்வோம், கோடுகளின் ஒப்பீட்டு நிலைக்கான விருப்பங்களைக் கருத்தில் கொள்வோம், மேலும் விண்வெளியில் ஒரு நேர் கோட்டை வரையறுப்பதற்கான முக்கிய முறைகளில் வாழ்வோம். சிறந்த புரிதலுக்காக, நாங்கள் கிராஃபிக் விளக்கப்படங்களை வழங்குகிறோம்.

பக்க வழிசெலுத்தல்.

விண்வெளியில் நேர்கோடு என்பது ஒரு கருத்து.

விண்வெளியில் இணையான கோடுகளின் வரையறையை வழங்கிய பிறகு, அவற்றின் முக்கியத்துவம் காரணமாக ஒரு நேர்கோட்டின் திசை திசையன்களைப் பற்றி பேச வேண்டும். பூஜ்ஜியமற்ற திசையன் இந்தக் கோட்டில் அல்லது இதற்கு இணையாக இருக்கும் ஒரு கோட்டின் மீது இருக்கும் எந்த ஒரு திசையன் கோட்டின் திசை திசையன் என்று அழைக்கப்படும். ஒரு நேர் கோட்டின் திசை திசையன் விண்வெளியில் ஒரு நேர் கோடு சம்பந்தப்பட்ட சிக்கல்களைத் தீர்க்கும் போது அடிக்கடி பயன்படுத்தப்படுகிறது.

இறுதியாக, முப்பரிமாண இடைவெளியில் இரண்டு கோடுகள் வெட்டும். விண்வெளியில் இரண்டு கோடுகள் ஒரே விமானத்தில் படாமல் இருந்தால், அவை வளைவு என்று அழைக்கப்படுகின்றன. விண்வெளியில் இரண்டு கோடுகளின் இந்த ஒப்பீட்டு நிலை, வெட்டும் கோடுகளுக்கு இடையில் ஒரு கோணத்தின் கருத்துக்கு நம்மை இட்டுச் செல்கிறது.

விண்வெளியில் ஒரு நேர் கோட்டை வரையறுப்பதற்கான முறைகள்.

விண்வெளியில் ஒரு நேர்கோட்டை தனித்துவமாக தீர்மானிக்க பல வழிகள் உள்ளன. முக்கியவற்றை பட்டியலிடுவோம்.

ஒரு நேர் கோடு இரண்டு புள்ளிகள் வழியாக செல்கிறது, ஒரே ஒரு புள்ளியை மட்டுமே நாம் அறிவோம். இவ்வாறு, நாம் விண்வெளியில் இரண்டு புள்ளிகளைக் குறித்தால், அவற்றின் வழியாக செல்லும் நேர்கோட்டை சந்தேகத்திற்கு இடமின்றி தீர்மானிக்க இது அனுமதிக்கும்.

ஒரு செவ்வக ஒருங்கிணைப்பு அமைப்பு முப்பரிமாண இடைவெளியில் அறிமுகப்படுத்தப்பட்டு, அதன் இரண்டு புள்ளிகளின் ஆயங்களைக் குறிப்பதன் மூலம் ஒரு நேர் கோடு குறிப்பிடப்பட்டால், கொடுக்கப்பட்ட இரண்டு புள்ளிகள் வழியாக செல்லும் ஒரு நேர்கோட்டிற்கான சமன்பாட்டை உருவாக்க நமக்கு வாய்ப்பு உள்ளது.

விண்வெளியில் ஒரு கோட்டை வரையறுப்பதற்கான இரண்டாவது முறை தேற்றத்தை அடிப்படையாகக் கொண்டது: கொடுக்கப்பட்ட கோட்டில் இல்லாத இடத்தில் எந்தப் புள்ளியிலும், கொடுக்கப்பட்ட வரிக்கு இணையாக ஒரு கோடு செல்கிறது, மேலும் ஒன்று மட்டுமே.

எனவே, நாம் ஒரு கோடு (அல்லது இந்த வரியின் ஒரு பகுதி) மற்றும் அதன் மீது பொய் இல்லாத ஒரு புள்ளியைக் குறிப்பிட்டால், கொடுக்கப்பட்ட ஒன்றிற்கு இணையான மற்றும் கொடுக்கப்பட்ட புள்ளியைக் கடந்து செல்லும் ஒரு கோட்டை தனித்துவமாக வரையறுப்போம்.

கோடு கடந்து செல்லும் புள்ளி மற்றும் அதன் திசை திசையன் ஆகியவற்றை நீங்கள் குறிப்பிடலாம். இது நேர்கோட்டை சந்தேகத்திற்கு இடமின்றி தீர்மானிக்க உங்களை அனுமதிக்கும்.

நிலையான செவ்வக ஒருங்கிணைப்பு அமைப்புடன் தொடர்புடைய ஒரு நேர் கோடு இந்த வழியில் குறிப்பிடப்பட்டால், விண்வெளியில் ஒரு நேர் கோட்டின் நியதிச் சமன்பாடுகளையும் விண்வெளியில் ஒரு நேர் கோட்டின் அளவுரு சமன்பாடுகளையும் உடனடியாக எழுதலாம்.

விண்வெளியில் ஒரு கோட்டை வரையறுப்பதற்கான பின்வரும் முறை ஸ்டீரியோமெட்ரியின் கோட்பாட்டை அடிப்படையாகக் கொண்டது: இரண்டு விமானங்களுக்கு ஒரு பொதுவான புள்ளி இருந்தால், இந்த விமானங்களின் அனைத்து பொதுவான புள்ளிகளும் இருக்கும் ஒரு பொதுவான நேர்கோடு உள்ளது.

இவ்வாறு, இரண்டு வெட்டும் விமானங்களை வரையறுப்பதன் மூலம், விண்வெளியில் ஒரு நேர் கோட்டை தனித்துவமாக வரையறுக்கிறோம்.

விண்வெளியில் ஒரு கோட்டை வரையறுப்பதற்கான மற்றொரு வழி தேற்றத்திலிருந்து பின்பற்றப்படுகிறது (இந்த கட்டுரையின் முடிவில் பட்டியலிடப்பட்டுள்ள புத்தகங்களில் அதன் ஆதாரத்தை நீங்கள் காணலாம்): ஒரு விமானம் மற்றும் அதில் இல்லாத ஒரு புள்ளி கொடுக்கப்பட்டால், ஒரு ஒற்றை வரி கடந்து செல்கிறது. இந்த புள்ளியின் வழியாக மற்றும் கொடுக்கப்பட்ட விமானத்திற்கு செங்குத்தாக.

எனவே, ஒரு நேர்கோட்டை தீர்மானிக்க, விரும்பிய நேர்கோடு செங்குத்தாக இருக்கும் விமானத்தையும் இந்த நேர்கோடு கடந்து செல்லும் புள்ளியையும் நீங்கள் குறிப்பிடலாம்.

அறிமுகப்படுத்தப்பட்ட செவ்வக ஒருங்கிணைப்பு அமைப்புடன் தொடர்புடைய ஒரு வரி இந்த வழியில் குறிப்பிடப்பட்டால், கொடுக்கப்பட்ட விமானத்திற்கு செங்குத்தாக கொடுக்கப்பட்ட புள்ளியின் வழியாக செல்லும் ஒரு கோட்டின் சமன்பாடு குறித்த கட்டுரையின் பொருளை அறிந்து கொள்வது பயனுள்ளதாக இருக்கும்.

நூல் பட்டியல்.

• அதனஸ்யன் எல்.எஸ்., புட்யூசோவ் வி.எஃப்., கடோம்ட்சேவ் எஸ்.பி., போஸ்னியாக் ஈ.ஜி., யுடினா ஐ.ஐ. வடிவியல். வகுப்புகள் 7 - 9: பொதுக் கல்வி நிறுவனங்களுக்கான பாடநூல்.
• அதனஸ்யன் எல்.எஸ்., புட்யூசோவ் வி.எஃப்., கடோம்ட்சேவ் எஸ்.பி., கிசெலேவா எல்.எஸ்., போஸ்னியாக் ஈ.ஜி. வடிவியல். மேல்நிலைப் பள்ளியின் 10-11 வகுப்புகளுக்கான பாடநூல்.
• புக்ரோவ் யா.எஸ்., நிகோல்ஸ்கி எஸ்.எம். உயர் கணிதம். தொகுதி ஒன்று: நேரியல் இயற்கணிதம் மற்றும் பகுப்பாய்வு வடிவவியலின் கூறுகள்.
• Ilyin V.A., Poznyak E.G. பகுப்பாய்வு வடிவியல்.

புத்திசாலி மாணவர்களின் பதிப்புரிமை

அனைத்து உரிமைகளும் பாதுகாக்கப்பட்டவை.
பதிப்புரிமை சட்டத்தால் பாதுகாக்கப்படுகிறது. உள் பொருட்கள் மற்றும் தோற்றம் உட்பட தளத்தின் எந்தப் பகுதியும், பதிப்புரிமைதாரரின் முன் எழுத்துப்பூர்வ அனுமதியின்றி, எந்த வடிவத்திலும் மீண்டும் உருவாக்கப்படக்கூடாது அல்லது பயன்படுத்தப்படக்கூடாது.