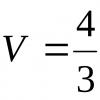One of the important operating parameters of any device, for which the efficiency of energy conversion is of particular importance, is the efficiency. By definition, the utility of equipment is determined by the ratio of useful energy to maximum energy and is expressed as a coefficient η. This, in a simplified sense, is the desired coefficient, the efficiency of the refrigerator and heater, which can be found in any technical instruction. In this case, you need to know some technical points.

Efficiency of the device and components

The efficiency factor, which is of most interest to readers, will not apply to the entire refrigeration device. Most often - an installed compressor that provides the necessary cooling parameters, or an engine. That is why, when wondering what the efficiency of a refrigerator is, we recommend asking about the installed compressor and the percentage.

It is better to consider this issue with an example. For example, there is an Ariston MB40D2NFE refrigerator (2003), which has a proprietary Danfoss NLE13KK.3 R600a compressor installed, with a power of 219W at operating temperature conditions of -23.3°C. In the case of refrigeration compressors, it may depend on the RC parameter (run capacitor), in our case it is 1.51 (without RC, -23.3°C) and 1.60 (with RC, -23.3°C). These data can be found in the technical parameters. The effect of a capacitor on the operation of the device is that it allows the operating speed to be reached faster and thus increases its useful effect.

The motor efficiency of your refrigeration unit is related to power and energy consumption. Obviously, the lower the coefficient, the more electricity the model consumes, the less efficient it is. That is, the maximum coefficient can be indirectly determined by the energy consumption class - A+++.

Compressor efficiency factor is above 1 – how and why?

Often the question of the useful action coefficient worries people who remember a little of their school physics course and cannot understand why the useful action is more than 100%. This question requires a little excursion into physics. The question concerns whether the efficiency factor of a thermal generator can be greater than 1?

This issue was clearly raised among professionals in 2006, when it was published in “Arguments and Facts” number 8 that vortex heat generators are capable of producing 172%. Despite the echoes of knowledge from a physics course, where efficiency is always less than 1, such a parameter is possible, but under certain conditions. We are talking specifically about the properties of the Carnot cycle.

In 1824, the French engineer S. Carnot examined and described one circular process, which subsequently played a decisive role in the development of thermodynamics and the use of thermal processes in technology. The Carnot cycle consists of two isotherms and two adiabats.

It is performed by gas in a cylinder with a piston, and the efficiency coefficient is expressed through the parameters of the heater and refrigerator and forms a ratio. A special feature is the fact that heat can transfer between heat exchangers without performing work by the piston, for this reason the Carnot cycle is considered the most efficient process that can be simulated under the conditions of the necessary heat exchange. In other words, the useful effect of the refrigeration unit with the implemented Carnot cycle will be the highest, or more precisely, the maximum.

If this part of the theory is remembered by many from the school course, then the rest is often lost behind the scenes. The main idea is that this cycle can be completed in any direction. A heat engine usually operates in a forward cycle, and refrigeration units operate in a reverse cycle, when heat is reduced in a cold reservoir and transferred to a hot one due to an external source of work - a compressor.

A situation where the utility coefficient is greater than 1 occurs if it is calculated from another utility coefficient, namely the ratio W(received)/W(spent) under one condition. It consists in the fact that expended energy means only useful energy that is used for real costs. As a result, in the thermodynamic cycles of heat pumps it is possible to determine energy costs that will be less than the volume of heat produced. Thus, with useful equipment less than 1, the efficiency of the heat pump can be greater.

Thermodynamic efficiency is always less than 1

In refrigeration (heat) machines, the formula usually considers the thermodynamic efficiency and refrigeration coefficient. In refrigeration units, this coefficient implies the efficiency of the cycle for obtaining useful work when heat is supplied to the working device from an external source (heat transmitter) and removed in another section of the heat circuit for the purpose of transfer to another external receiver.

In total, the working fluid undergoes two processes - expansion and compression, which correspond to the work parameter. The most efficient device is considered when the heat supplied is less than the heat removed - the more pronounced the efficiency of the cycle will be.

The degree of perfection of a thermodynamic device that converts heat into mechanical work is estimated by the thermal coefficient as a percentage, which may be of interest in this case. Thermal efficiency usually measures and measures how much heat from the heater and refrigerator the machine converts into operation under specific conditions that are considered ideal. The value of the thermal parameter is always less than 1 and cannot be higher, as is the case with compressors. At 40° temperature the device will operate with minimal efficiency.

Eventually

In modern household refrigeration units, it is the reverse Carnot process that is used, and the temperature of the refrigerator can be determined depending on the amount of heat transferred from the heating element. The parameters of the cooling chamber and heaters can be completely different in practice, and also depend on the external operation of the engine with the compressor, which has its own efficiency parameter. Accordingly, these parameters (refrigerator efficiency as a percentage) with a fundamentally identical thermodynamic process will depend on the technology implemented by the manufacturer.

Since, according to the formula, the utility coefficient depends on the temperatures of the heat exchangers, the technical parameters indicate what percentage of utility can be obtained under certain ideal conditions. It is this data that can be used to compare models of different brands not only based on photos, including those operating under normal conditions or in heat up to 40°.

Efficiency factor (efficiency) is a term that can be applied to, perhaps, every system and device. Even a person has an efficiency factor, although there is probably no objective formula for finding it yet. In this article we will explain in detail what efficiency is and how it can be calculated for various systems.

Efficiency definition

Efficiency is an indicator that characterizes the effectiveness of a system in terms of energy output or conversion. Efficiency is an immeasurable quantity and is represented either as a numerical value in the range from 0 to 1, or as a percentage.

General formula

Efficiency is indicated by the symbol Ƞ.

The general mathematical formula for finding efficiency is written as follows:

Ƞ=A/Q, where A is the useful energy/work performed by the system, and Q is the energy consumed by this system to organize the process of obtaining useful output.

The efficiency factor, unfortunately, is always less than or equal to unity, since, according to the law of conservation of energy, we cannot obtain more work than the energy expended. In addition, the efficiency, in fact, is extremely rarely equal to unity, since useful work is always accompanied by losses, for example, for heating the mechanism.

Heat engine efficiency

A heat engine is a device that converts thermal energy into mechanical energy. In a heat engine, work is determined by the difference between the amount of heat received from the heater and the amount of heat given to the cooler, and therefore the efficiency is determined by the formula:

• Ƞ=Qн-Qх/Qн, where Qн is the amount of heat received from the heater, and Qх is the amount of heat given to the cooler.

It is believed that the highest efficiency is provided by engines operating on the Carnot cycle. In this case, the efficiency is determined by the formula:

• Ƞ=T1-T2/T1, where T1 is the temperature of the hot spring, T2 is the temperature of the cold spring.

Electric motor efficiency

An electric motor is a device that converts electrical energy into mechanical energy, so efficiency in this case is the efficiency ratio of the device in converting electrical energy into mechanical energy. The formula for finding the efficiency of an electric motor looks like this:

• Ƞ=P2/P1, where P1 is the supplied electrical power, P2 is the useful mechanical power generated by the engine.

Electrical power is found as the product of system current and voltage (P=UI), and mechanical power as the ratio of work per unit time (P=A/t)

Transformer efficiency

A transformer is a device that converts alternating current of one voltage to alternating current of another voltage while maintaining the frequency. In addition, transformers can also convert alternating current into direct current.

The efficiency of the transformer is found by the formula:

• Ƞ=1/1+(P0+PL*n2)/(P2*n), where P0 is the no-load loss, PL is the load loss, P2 is the active power supplied to the load, n is the relative degree of load.

Efficiency or not efficiency?

It is worth noting that in addition to efficiency, there are a number of indicators that characterize the efficiency of energy processes, and sometimes we can come across descriptions like - efficiency of the order of 130%, however in this case we need to understand that the term is not used entirely correctly, and, most likely, the author or the manufacturer understands this abbreviation to mean a slightly different characteristic.

For example, heat pumps are distinguished by the fact that they can release more heat than they consume. Thus, a refrigeration machine can remove more heat from the object being cooled than was expended in energy equivalent to organize the removal. The efficiency indicator of a refrigeration machine is called the refrigeration coefficient, denoted by the letter Ɛ and determined by the formula: Ɛ=Qx/A, where Qx is the heat removed from the cold end, A is the work expended on the removal process. However, sometimes the refrigeration coefficient is also called the efficiency of the refrigeration machine.

It is also interesting that the efficiency of boilers operating on organic fuel is usually calculated based on the lower calorific value, and it can be greater than unity. However, it is still traditionally called efficiency. It is possible to determine the efficiency of a boiler by the higher calorific value, and then it will always be less than one, but in this case it will be inconvenient to compare the performance of boilers with data from other installations.

>>Physics: The principle of operation of heat engines. Coefficient of performance (efficiency) of heat engines

The reserves of internal energy in the earth's crust and oceans can be considered practically unlimited. But to solve practical problems, having energy reserves is not enough. It is also necessary to be able to use energy to set in motion machine tools in factories and factories, vehicles, tractors and other machines, to rotate the rotors of electric current generators, etc. Humanity needs engines - devices capable of doing work. Most of the engines on Earth are heat engines. Heat engines are devices that convert the internal energy of fuel into mechanical energy.
Operating principles of heat engines. In order for an engine to do work, there needs to be a pressure difference on both sides of the engine piston or turbine blades. In all heat engines, this pressure difference is achieved by increasing the temperature of the working fluid (gas) by hundreds or thousands of degrees compared to the ambient temperature. This temperature increase occurs when fuel burns.
One of the main parts of the engine is a gas-filled vessel with a movable piston. The working fluid of all heat engines is gas, which does work during expansion. Let us denote the initial temperature of the working fluid (gas) by T 1. This temperature in steam turbines or machines is achieved by the steam in the steam boiler. In internal combustion engines and gas turbines, the temperature rise occurs as fuel burns inside the engine itself. Temperature T 1 heater temperature."
The role of the refrigerator. As work is done, the gas loses energy and inevitably cools to a certain temperature. T 2, which is usually slightly higher than the ambient temperature. They call her refrigerator temperature. The refrigerator is the atmosphere or special devices for cooling and condensing waste steam - capacitors. In the latter case, the temperature of the refrigerator may be slightly lower than the atmospheric temperature.
Thus, in an engine, the working fluid during expansion cannot give up all its internal energy to do work. Some of the heat is inevitably transferred to the refrigerator (atmosphere) along with waste steam or exhaust gases from internal combustion engines and gas turbines. This part of the internal energy is lost.
A heat engine performs work using the internal energy of the working fluid. Moreover, in this process, heat is transferred from hotter bodies (heater) to colder ones (refrigerator).
The schematic diagram of a heat engine is shown in Figure 13.11.
The working fluid of the engine receives heat from the heater during fuel combustion Q 1 does work A´ and transfers the amount of heat to the refrigerator Q 2 .
Coefficient of performance (efficiency) of a heat engine The impossibility of completely converting the internal energy of gas into the work of heat engines is due to the irreversibility of processes in nature. If heat could return spontaneously from the refrigerator to the heater, then the internal energy could be completely converted into useful work by any heat engine.
According to the law of conservation of energy, the work done by the engine is equal to:

Where Q 1- the amount of heat received from the heater, and Q 2- the amount of heat transferred to the refrigerator.
Coefficient of performance (efficiency) of a heat engine called work attitude A´ performed by the engine to the amount of heat received from the heater:

Since all engines transfer some amount of heat to the refrigerator, then η<1.
The efficiency of a heat engine is proportional to the temperature difference between the heater and the refrigerator. At T 1 -T 2=0 The motor cannot run.
Maximum efficiency value of heat engines. The laws of thermodynamics make it possible to calculate the maximum possible efficiency of a heat engine operating with a heater having a temperature T 1, and a refrigerator with a temperature T 2. This was first done by the French engineer and scientist Sadi Carnot (1796-1832) in his work “Reflections on the driving force of fire and on machines capable of developing this force” (1824).
Carnot came up with an ideal heat engine with an ideal gas as a working fluid. An ideal Carnot heat engine operates on a cycle consisting of two isotherms and two adiabats. First, a vessel with gas is brought into contact with a heater, the gas expands isothermally, performing positive work, at a temperature T1, at the same time he receives the amount of heat Q 1.
Then the vessel is thermally insulated, the gas continues to expand adiabatically, while its temperature drops to the temperature of the refrigerator T 2. After this, the gas is brought into contact with the refrigerator; during isothermal compression, it transfers an amount of heat to the refrigerator Q 2, shrinking to volume V 4 . Then the vessel is thermally insulated again, the gas is compressed adiabatically to volume V 1 and returns to its original state.
Carnot obtained the following expression for the efficiency of this machine:

As one would expect, the efficiency of a Carnot machine is directly proportional to the difference in the absolute temperatures of the heater and refrigerator.
The main significance of this formula is that any real heat engine operating with a heater having a temperature T1, and a refrigerator with a temperature T 2, cannot have an efficiency exceeding that of an ideal heat engine.

Formula (13.19) gives the theoretical limit for the maximum efficiency value of heat engines. It shows that the higher the temperature of the heater and the lower the temperature of the refrigerator, the more efficient a heat engine is. Only at a refrigerator temperature equal to absolute zero, η =1.
But the temperature of the refrigerator practically cannot be lower than the ambient temperature. You can increase the heater temperature. However, any material (solid body) has limited heat resistance, or heat resistance. When heated, it gradually loses its elastic properties, and at a sufficiently high temperature it melts.
Now the main efforts of engineers are aimed at increasing the efficiency of engines by reducing the friction of their parts, fuel losses due to incomplete combustion, etc. Real opportunities for increasing efficiency here still remain great. Thus, for a steam turbine, the initial and final steam temperatures are approximately as follows: T 1≈800 K and T 2≈300 K. At these temperatures, the maximum efficiency value is:

The actual efficiency value due to various types of energy losses is approximately 40%. The maximum efficiency - about 44% - is achieved by Diesel engines.
Increasing the efficiency of heat engines and bringing it closer to the maximum possible is the most important technical task.
Heat engines perform work due to the difference in gas pressure on the surfaces of the pistons or turbine blades. This pressure difference is created by a temperature difference. The maximum possible efficiency is proportional to this temperature difference and inversely proportional to the absolute temperature of the heater.
A heat engine cannot operate without a refrigerator, the role of which is usually played by the atmosphere.

???
1. What device is called a heat engine?
2. What is the role of the heater, cooler and working fluid in a heat engine?
3. What is the efficiency of the engine?
4. What is the maximum efficiency value of a heat engine?

G.Ya.Myakishev, B.B.Bukhovtsev, N.N.Sotsky, Physics 10th grade

Lesson content lesson notes supporting frame lesson presentation acceleration methods interactive technologies Practice tasks and exercises self-test workshops, trainings, cases, quests homework discussion questions rhetorical questions from students Illustrations audio, video clips and multimedia photographs, pictures, graphics, tables, diagrams, humor, anecdotes, jokes, comics, parables, sayings, crosswords, quotes Add-ons abstracts articles tricks for the curious cribs textbooks basic and additional dictionary of terms other Improving textbooks and lessonscorrecting errors in the textbook updating a fragment in a textbook, elements of innovation in the lesson, replacing outdated knowledge with new ones Only for teachers perfect lessons calendar plan for the year; methodological recommendations; discussion programs Integrated Lessons

If you have corrections or suggestions for this lesson,

The working fluid, receiving a certain amount of heat Q 1 from the heater, gives part of this amount of heat, equal in modulus |Q2|, to the refrigerator. Therefore, the work done cannot be greater A = Q 1- |Q 2 |. The ratio of this work to the amount of heat received by the expanding gas from the heater is called efficiency heat engine:

The efficiency of a heat engine operating in a closed cycle is always less than one. The task of thermal power engineering is to make the efficiency as high as possible, that is, to use as much of the heat received from the heater as possible to produce work. How can this be achieved?
For the first time, the most perfect cyclic process, consisting of isotherms and adiabats, was proposed by the French physicist and engineer S. Carnot in 1824.

Carnot cycle.

Let us assume that the gas is in a cylinder, the walls and piston of which are made of a heat-insulating material, and the bottom is made of a material with high thermal conductivity. The volume occupied by the gas is equal to V 1.

Figure 2

Let's bring the cylinder into contact with the heater (Figure 2) and give the gas the opportunity to expand isothermally and do work . The gas receives a certain amount of heat from the heater Q 1. This process is graphically represented by an isotherm (curve AB).

Figure 3

When the volume of gas becomes equal to a certain value V 1'< V 2 , the bottom of the cylinder is isolated from the heater , After this, the gas expands adiabatically to the volume V 2, corresponding to the maximum possible stroke of the piston in the cylinder (adiabatic Sun). In this case, the gas is cooled to a temperature T 2< T 1 .
The cooled gas can now be compressed isothermally at a temperature T2. To do this, it must be brought into contact with a body having the same temperature T 2, i.e. with a refrigerator , and compress the gas by an external force. However, in this process the gas will not return to its original state - its temperature will always be lower than T 1.
Therefore, isothermal compression is brought to a certain intermediate volume V 2 '>V 1(isotherm CD). In this case, the gas gives off some heat to the refrigerator Q2, equal to the work of compression performed on it. After this, the gas is compressed adiabatically to a volume V 1, at the same time its temperature rises to T 1(adiabatic D.A.). Now the gas has returned to its original state, in which its volume is equal to V 1, temperature - T1, pressure - p 1, and the cycle can be repeated again.

So, on the site ABC gas does work (A > 0), and on the site CDA work done on the gas (A< 0). At the sites Sun And AD work is done only by changing the internal energy of the gas. Since the change in internal energy UBC = – UDA, then the work during adiabatic processes is equal: ABC = –ADA. Consequently, the total work done per cycle is determined by the difference in work done during isothermal processes (sections AB And CD). Numerically, this work is equal to the area of ​​the figure bounded by the cycle curve ABCD.
Only part of the amount of heat is actually converted into useful work QT, received from the heater, equal to QT 1 – |QT 2 |. So, in the Carnot cycle, useful work A = QT 1– |QT 2 |.
The maximum efficiency of an ideal cycle, as shown by S. Carnot, can be expressed in terms of the heater temperature (T 1) and refrigerator (T 2):

In real engines it is not possible to implement a cycle consisting of ideal isothermal and adiabatic processes. Therefore, the efficiency of the cycle carried out in real engines is always less than the efficiency of the Carnot cycle (at the same temperatures of heaters and refrigerators):

The formula shows that the higher the heater temperature and the lower the refrigerator temperature, the greater the engine efficiency.

Carnot Nicolas Leonard Sadi (1796-1832) - a talented French engineer and physicist, one of the founders of thermodynamics. In his work “Reflections on the driving force of fire and on machines capable of developing this force” (1824), he first showed that heat engines can perform work only in the process of transferring heat from a hot body to a cold one. Carnot came up with an ideal heat engine, calculated the efficiency of the ideal machine and proved that this coefficient is the maximum possible for any real heat engine.
As an aid to his research, Carnot invented (on paper) in 1824 an ideal heat engine with an ideal gas as the working fluid. The important role of the Carnot engine lies not only in its possible practical application, but also in the fact that it allows us to explain the principles of operation of heat engines in general; It is equally important that Carnot, with the help of his engine, managed to make a significant contribution to the substantiation and understanding of the second law of thermodynamics. All processes in a Carnot machine are considered as equilibrium (reversible). A reversible process is a process that proceeds so slowly that it can be considered as a sequential transition from one equilibrium state to another, etc., and this entire process can be carried out in the opposite direction without changing the work done and the amount of heat transferred. (Note that all real processes are irreversible) A circular process or cycle is carried out in the machine, in which the system, after a series of transformations, returns to its original state. The Carnot cycle consists of two isotherms and two adiabats. Curves A - B and C - D are isotherms, and B - C and D - A are adiabats. First, the gas expands isothermally at temperature T 1 . At the same time, it receives the amount of heat Q 1 from the heater. Then it expands adiabatically and does not exchange heat with the surrounding bodies. This is followed by isothermal compression of the gas at temperature T 2 . In this process, the gas transfers the amount of heat Q 2 to the refrigerator. Finally, the gas is compressed adiabatically and returns to its original state. During isothermal expansion, the gas does work A" 1 >0, equal to the amount of heat Q 1. With adiabatic expansion B - C, positive work A" 3 is equal to the decrease in internal energy when the gas is cooled from temperature T 1 to temperature T 2: A" 3 =- dU 1.2 =U(T 1)-U(T 2). Isothermal compression at temperature T 2 requires work A 2 to be performed on the gas. The gas performs correspondingly negative work A" 2 = -A 2 = Q 2. Finally, adiabatic compression requires work done on the gas A 4 = dU 2.1. The work of the gas itself A" 4 = -A 4 = -dU 2.1 = U(T 2) -U(T 1). Therefore, the total work of the gas during two adiabatic processes is zero. During the cycle, the gas does work A" = A" 1 + A" 2 =Q 1 +Q 2 =|Q 1 |-|Q 2 |. This work is numerically equal to the area of ​​the figure limited by the cycle curve. To calculate the efficiency, it is necessary to calculate the work for isothermal processes A - B and C - D. Calculations lead to the following result: (2) The efficiency of a Carnot heat engine is equal to the ratio of the difference between the absolute temperatures of the heater and refrigerator to the absolute temperature of the heater. The main significance of Carnot's formula (2) for the efficiency of an ideal machine is that it determines the maximum possible efficiency of any heat engine. Carnot proved the following theorem: any real heat engine operating with a heater at temperature T 1 and a refrigerator at temperature T 2 cannot have an efficiency that exceeds the efficiency of an ideal heat engine. Efficiency of real heat engines Formula (2) gives the theoretical limit for the maximum value of the efficiency of heat engines. It shows that the higher the temperature of the heater and the lower the temperature of the refrigerator, the more efficient a heat engine is. Only at a refrigerator temperature equal to absolute zero does the efficiency equal 1. In real heat engines, processes proceed so quickly that the decrease and increase in the internal energy of the working substance when its volume changes does not have time to be compensated by the influx of energy from the heater and the release of energy to the refrigerator. Therefore, isothermal processes cannot be realized. The same applies to strictly adiabatic processes, since there are no ideal heat insulators in nature. The cycles carried out in real heat engines consist of two isochores and two adiabats (in the Otto cycle), of two adiabats, isobars and isochores (in the Diesel cycle), of two adiabats and two isobars (in a gas turbine), etc. In this case, one should have keeping in mind that these cycles can also be ideal, like the Carnot cycle. But for this it is necessary that the temperatures of the heater and refrigerator are not constant, as in the Carnot cycle, but change in the same way as the temperature of the working substance changes in the processes of isochoric heating and cooling. In other words, the working substance must be in contact with an infinitely large number of heaters and refrigerators - only in this case there will be equilibrium heat transfer at the isochores. Of course, in the cycles of real heat engines, the processes are nonequilibrium, as a result of which the efficiency of real heat engines at the same temperature range is significantly less than the efficiency of the Carnot cycle. At the same time, expression (2) plays a huge role in thermodynamics and is a kind of “beacon” indicating ways to increase the efficiency of real heat engines.
	In the Otto cycle, the working mixture is first sucked into the cylinder 1-2, then adiabatic compression 2-3 and after its isochoric combustion 3-4, accompanied by an increase in the temperature and pressure of the combustion products, their adiabatic expansion 4-5 occurs, then an isochoric pressure drop 5 -2 and isobaric expulsion of exhaust gases by the piston 2-1. Since no work is done on isochores, and the work during suction of the working mixture and expulsion of exhaust gases is equal and opposite in sign, the useful work for one cycle is equal to the difference in work on the adiabats of expansion and compression and is graphically depicted by the area of ​​the cycle.
Comparing the efficiency of a real heat engine with the efficiency of the Carnot cycle, it should be noted that in expression (2) the temperature T 2 in exceptional cases may coincide with the ambient temperature, which we take for a refrigerator, but in the general case it exceeds the ambient temperature. So, for example, in internal combustion engines, T2 should be understood as the temperature of the exhaust gases, and not the temperature of the environment into which the exhaust is produced.
	The figure shows the cycle of a four-stroke internal combustion engine with isobaric combustion (Diesel cycle). Unlike the previous cycle, in section 1-2 it is absorbed. atmospheric air, which is subjected to adiabatic compression in section 2-3 to 3 10 6 -3 10 5 Pa. The injected liquid fuel ignites in an environment of highly compressed, and therefore heated, air and burns isobarically 3-4, and then an adiabatic expansion of the combustion products 4-5 occurs. The remaining processes 5-2 and 2-1 proceed in the same way as in the previous cycle. It should be remembered that in internal combustion engines the cycles are conditionally closed, since before each cycle the cylinder is filled with a certain mass of working substance, which is ejected from the cylinder at the end of the cycle.
But the temperature of the refrigerator practically cannot be much lower than the ambient temperature. You can increase the heater temperature. However, any material (solid body) has limited heat resistance, or heat resistance. When heated, it gradually loses its elastic properties, and at a sufficiently high temperature it melts. Now the main efforts of engineers are aimed at increasing the efficiency of engines by reducing the friction of their parts, fuel losses due to incomplete combustion, etc. Real opportunities for increasing efficiency here still remain great. So, for a steam turbine, the initial and final temperatures of the steam are approximately the following: T 1 = 800 K and T 2 = 300 K. At these temperatures, the maximum value of the efficiency coefficient is: The actual efficiency value due to various types of energy losses is approximately 40%. The maximum efficiency - about 44% - is achieved by internal combustion engines. The efficiency of any heat engine cannot exceed the maximum possible value where T 1 is the absolute temperature of the heater, and T 2 is the absolute temperature of the refrigerator. Increasing the efficiency of heat engines and bringing it closer to the maximum possible is the most important technical task.

Clausius inequality

(1854): The amount of heat obtained by a system in any circular process, divided by the absolute temperature at which it was received ( given amount of heat), non-positive.

The amount of heat supplied quasi-statically received by the system does not depend on the transition path (determined only by the initial and final states of the system) - for quasi-static processes The Clausius inequality turns into equality .

Entropy, state function S thermodynamic system, the change of which dS for an infinitesimal reversible change in the state of the system is equal to the ratio of the amount of heat received by the system in this process (or taken away from the system) to the absolute temperature T:

Magnitude dS is a total differential, i.e. its integration along any arbitrarily chosen path gives the difference between the values entropy in the initial (A) and final (B) states:

Heat is not a function of state, so the integral of δQ depends on the chosen transition path between states A and B. Entropy measured in J/(mol deg).

Concept entropy as a function of the state of the system is postulated second law of thermodynamics, which is expressed through entropy difference between irreversible and reversible processes. For the first dS>δQ/T for the second dS=δQ/T.

Entropy as a function internal energy U system, volume V and number of moles n i i th component is a characteristic function (see. Thermodynamic potentials). This is a consequence of the first and second laws of thermodynamics and is written by the equation:

Where R - pressure, μ i - chemical potential i th component. Derivatives entropy by natural variables U, V And n i are equal:

Simple formulas connect entropy with heat capacities at constant pressure S p and constant volume Cv:

By using entropy conditions are formulated for achieving thermodynamic equilibrium of a system at constant internal energy, volume and number of moles i th component (isolated system) and the stability condition for such equilibrium:

It means that entropy of an isolated system reaches a maximum in a state of thermodynamic equilibrium. Spontaneous processes in the system can only occur in the direction of increasing entropy.

Entropy belongs to a group of thermodynamic functions called Massier-Planck functions. Other functions belonging to this group are the Massier function F 1 = S - (1/T)U and Planck function Ф 2 = S - (1/T)U - (p/T)V, can be obtained by applying the Legendre transform to the entropy.

According to the third law of thermodynamics (see. Thermal theorem), change entropy in a reversible chemical reaction between substances in a condensed state tends to zero at T→0:

Planck's postulate (an alternative formulation of the thermal theorem) states that entropy of any chemical compound in a condensed state at absolute zero temperature is conditionally zero and can be taken as the starting point when determining the absolute value entropy substances at any temperature. Equations (1) and (2) define entropy up to a constant term.

In chemical thermodynamics The following concepts are widely used: standard entropy S 0, i.e. entropy at pressure R=1.01·10 5 Pa (1 atm); standard entropy chemical reaction i.e. standard difference entropies products and reagents; partial molar entropy component of a multicomponent system.

To calculate chemical equilibria, use the formula:

Where TO - equilibrium constant, and - respectively standard Gibbs energy, enthalpy and entropy of reaction; R- gas constant.

Definition of the concept entropy for a nonequilibrium system is based on the idea of ​​local thermodynamic equilibrium. Local equilibrium implies the fulfillment of equation (3) for small volumes of a system that is nonequilibrium as a whole (see. Thermodynamics of irreversible processes). During irreversible processes in the system, production (occurrence) can occur entropy. Full differential entropy is determined in this case by the Carnot-Clausius inequality:

Where dS i > 0 - differential entropy, not related to heat flow but due to production entropy due to irreversible processes in the system ( diffusion. thermal conductivity, chemical reactions, etc.). Local production entropy (t- time) is represented as the sum of products of generalized thermodynamic forces X i to generalized thermodynamic flows J i:

Production entropy due, for example, to the diffusion of a component i due to the force and flow of matter J; production entropy due to a chemical reaction - by force X=A/T, Where A-chemical affinity, and flow J, equal to the reaction rate. In statistical thermodynamics entropy isolated system is determined by the relation: where k - Boltzmann constant. - thermodynamic weight of the state, equal to the number of possible quantum states of the system with given values ​​of energy, volume, number of particles. The equilibrium state of the system corresponds to the equality of populations of single (non-degenerate) quantum states. Increasing entropy in irreversible processes is associated with the establishment of a more probable distribution of the given energy of the system among individual subsystems. Generalized statistical definition entropy, which also applies to non-isolated systems, connects entropy with the probabilities of various microstates as follows:

Where w i- probability i-th state.

Absolute entropy a chemical compound is determined experimentally, mainly by the calorimetric method, based on the ratio:

The use of the second principle allows us to determine entropy chemical reactions based on experimental data (electromotive force method, vapor pressure method, etc.). Calculation possible entropy chemical compounds using statistical thermodynamics methods, based on molecular constants, molecular weight, molecular geometry, and normal vibration frequencies. This approach is successfully carried out for ideal gases. For condensed phases, statistical calculations provide significantly less accuracy and are carried out in a limited number of cases; In recent years, significant progress has been made in this area.

Related information.

In the theoretical model of a heat engine, three bodies are considered: heater, working fluid And fridge.

Heater – a thermal reservoir (large body), the temperature of which is constant.

In each cycle of engine operation, the working fluid receives a certain amount of heat from the heater, expands and performs mechanical work. The transfer of part of the energy received from the heater to the refrigerator is necessary to return the working fluid to its original state.

Since the model assumes that the temperature of the heater and refrigerator does not change during the operation of the heat engine, then at the completion of the cycle: heating-expansion-cooling-compression of the working fluid, it is considered that the machine returns to its original state.

For each cycle, based on the first law of thermodynamics, we can write that the amount of heat Q heat received from the heater, amount of heat | Q cold| given to the refrigerator, and the work done by the working body A are related to each other by the relation:

A = Q heat – | Q cold|.

In real technical devices, which are called heat engines, the working fluid is heated by the heat released during the combustion of fuel. So, in a steam turbine of a power plant, the heater is a furnace with hot coal. In an internal combustion engine (ICE), combustion products can be considered a heater, and excess air can be considered a working fluid. They use atmospheric air or water from natural sources as a refrigerator.

Efficiency of a heat engine (machine)

Heat engine efficiency (efficiency) is the ratio of the work done by the engine to the amount of heat received from the heater:

The efficiency of any heat engine is less than unity and is expressed as a percentage. The impossibility of converting the entire amount of heat received from the heater into mechanical work is the price to pay for the need to organize a cyclic process and follows from the second law of thermodynamics.

In real heat engines, efficiency is determined by experimental mechanical power N engine and the amount of fuel burned per unit time. So, if during the time t mass of fuel burned m and specific heat of combustion q, That

For vehicles, the reference characteristic is often the volume V burned fuel on the way s at mechanical engine power N and at speed. In this case, taking into account the density r of the fuel, we can write the formula for calculating the efficiency:

Second law of thermodynamics

There are several formulations second law of thermodynamics. One of them says that it is impossible to have a heat engine that would do work only due to a heat source, i.e. no refrigerator. The world's oceans could serve for him as a practically inexhaustible source of internal energy (Wilhelm Friedrich Ostwald, 1901).

Other formulations of the second law of thermodynamics are equivalent to this one.

Clausius formulation(1850): a process in which heat would spontaneously transfer from less heated bodies to more heated bodies is impossible.

Thomson's formulation(1851): a circular process is impossible, the only result of which would be the production of work by reducing the internal energy of the thermal reservoir.

Clausius formulation(1865): all spontaneous processes in a closed nonequilibrium system occur in a direction in which the entropy of the system increases; in a state of thermal equilibrium it is maximum and constant.

Boltzmann formulation(1877): a closed system of many particles spontaneously passes from a more ordered state to a less ordered one. The system cannot spontaneously leave its equilibrium position. Boltzmann introduced a quantitative measure of disorder in a system consisting of many bodies - entropy.

Efficiency of a heat engine with an ideal gas as a working fluid

If a model of the working fluid in a heat engine is given (for example, an ideal gas), then it is possible to calculate the change in the thermodynamic parameters of the working fluid during expansion and compression. This allows the efficiency of a heat engine to be calculated based on the laws of thermodynamics.

The figure shows cycles for which the efficiency can be calculated if the working fluid is an ideal gas and the parameters are specified at the transition points of one thermodynamic process to another.

	Isobaric-isochoric
	Isochoric-adiabatic
	Isobaric-adiabatic
	Isobaric-isochoric-isothermal
	Isobaric-isochoric-linear

Carnot cycle. Efficiency of an ideal heat engine

Highest efficiency at given heater temperatures T heater and refrigerator T hall has a heat engine, where the working fluid expands and contracts according to Carnot cycle(Fig. 2), the graph of which consists of two isotherms (2–3 and 4–1) and two adiabats (3–4 and 1–2).

Carnot's theorem proves that the efficiency of such an engine does not depend on the working fluid used, so it can be calculated using the thermodynamic relations for an ideal gas:

Environmental consequences of heat engines

The intensive use of heat engines in transport and energy (thermal and nuclear power plants) significantly affects the Earth's biosphere. Although there are scientific disputes about the mechanisms of influence of human activity on the Earth's climate, many scientists note the factors due to which such an influence can occur:

1. The greenhouse effect is an increase in the concentration of carbon dioxide (a product of combustion in heaters of heat engines) in the atmosphere. Carbon dioxide allows visible and ultraviolet radiation from the Sun to pass through, but absorbs infrared radiation from the Earth into space. This leads to an increase in the temperature of the lower layers of the atmosphere, increased hurricane winds and global melting of ice.
2. Direct impact of toxic exhaust gases on wildlife (carcinogens, smog, acid rain from combustion by-products).
3. Destruction of the ozone layer during airplane flights and rocket launches. Ozone in the upper atmosphere protects all life on Earth from excess ultraviolet radiation from the Sun.

The way out of the emerging environmental crisis lies in increasing the efficiency of heat engines (the efficiency of modern heat engines rarely exceeds 30%); using serviceable engines and harmful exhaust gas neutralizers; the use of alternative energy sources (solar panels and heaters) and alternative means of transport (bicycles, etc.).

Read also...

• Compote with one-time filling
• Compote of ranetki and grapes for the winter
• Vegetable stew with potatoes and zucchini - a very tasty recipe
• Why do you dream about a kite?