Šajā nodarbībā mēs sniegsim pamata definīcijas un teorēmas par tēmu paralēlām taisnēm telpā.
Nodarbības sākumā aplūkosim paralēlo līniju definīciju telpā un pierādīsim teorēmu, ka caur jebkuru telpas punktu iespējams novilkt tikai vienu taisni paralēli dotajai. Tālāk mēs pierādīsim lemmu par divām paralēlām taisnēm, kas krustojas ar plakni. Un ar tās palīdzību mēs pierādīsim teorēmu par divām taisnēm, kas ir paralēlas trešajai taisnei.

Tēma: Līniju un plakņu paralēlisms

Nodarbība: Paralēlas līnijas telpā. Trīs līniju paralēlisms

Mēs jau esam pētījuši paralēlas līnijas planimetrijā. Tagad mums ir jādefinē paralēlas līnijas telpā un jāpierāda atbilstošās teorēmas.

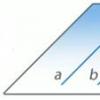
Definīcija: divas līnijas telpā sauc par paralēlām, ja tās atrodas vienā plaknē un nekrustojas (1. att.).

Paralēlo līniju apzīmējums: a || b.

1. Kuras taisnes sauc par paralēlām?

2. Pierādīt, ka visas taisnes, kas krusto divas noteiktas paralēlas taisnes, atrodas vienā plaknē.

3. Līnija krusto taisnes AB Un B.C. taisnā leņķī. Vai līnijas ir paralēlas? AB Un B.C.?

4. Ģeometrija. 10.-11.klase: mācību grāmata vispārējās izglītības iestāžu audzēkņiem (pamata un specializācijas līmeņi) / I. M. Smirnova, V. A. Smirnovs. - 5. izdevums, labots un paplašināts - M.: Mnemosyne, 2008. - 288 lpp. : slim.

Ja divas taisnes krustojas vai ir paralēlas, tad tās atrodas vienā plaknē. Tomēr telpā divas līnijas var atrasties tā, lai tās neatrastos vienā plaknē, tas ir, nav plaknes, kas iet caur abām šīm līnijām. Ir skaidrs, ka šādas līnijas nekrustojas vai ir paralēlas.

Telpā aplūkoti trīs iespējamie divu taisnu līniju izkārtojuma gadījumi. Divas taisnas līnijas telpā var:

1. Atrodas vienā plaknē un ir kopīgs punkts;

2. Atrodas vienā plaknē un nav kopīgu punktu;

Negulieties vienā plaknē un tāpēc tiem nav kopīgu punktu.

Definīcija: Tiek uzskatīts, ka divas līnijas krustojas, ja tām ir kopīgs punkts.

Definīcija: divas taisnes sauc par paralēlām, ja tās atrodas vienā plaknē un tām nav kopīgu punktu vai tās nesakrīt.

Definīcija: divas taisnes sauc par šķībām, ja tās nekrustojas un nav paralēlas (neatrodas vienā plaknē).

Apzīmējums:a · b

TAISNĪJU KRUSTOŠANAS ZĪME

Teorēma: ja viena no divām taisnēm atrodas plaknē, bet otra šķērso šo plakni punktā, kas nepieder pie pirmās taisnes, tad šīs taisnes krustojas.

Ņemot vērā: ; ; .

Pierādīt:a · b

Pierādījums: (pretrunīgi)

Pieņemsim pretējo tam, ko vēlamies pierādīt, tas ir, ka šīs taisnes krustojas vai ir paralēlas: .

Vienu plakni var novilkt caur divām krustojošām vai paralēlām taisnēm, tāpēc ir noteikta plakne, kurā atrodas šīs taisnes: .

Atbilstoši teorēmas nosacījumiem.

Pēc pieņēmuma.

No teorēmas nosacījumiem un pieņēmuma izriet, ka abas plaknes iet caur taisni “a” un tai nepiederošo punktu M Un tā kā caur taisni var izvilkt vienu un tikai vienu plakni un punktu, kas tai nepieder, tāpēc plaknes sakrīt. .

Pēc pieņēmuma.

Pēc nosacījuma.

Mēs saņēmām pretrunu ar teorēmas nosacījumiem, tāpēc pieņēmums nav patiess, bet tas, kas bija jāpierāda, ir patiess, tas ir, līnijas krustojas: a · b.

Atcerieties, ka leņķis starp krustojošām līnijām ir leņķis starp paralēlām līnijām, kas iet caur vienu punktu. Citiem vārdiem sakot, ja taisni l o un l 1 ir šķērsoti, tad mums ir jāveic līnijas paralēlais tulkojums l o , lai tā izrādītos taisna līnija l o ¢ krustojas ar l 1, un izmēriet leņķi starp l o ¢ un l 1 .

Divām šķībām līnijām ir viens kopīgs perpendikuls. Tā garumu sauc par attālumu starp līnijām.

Divas telpas līnijas definē ar to kanoniskajiem vienādojumiem:

l o: = = , l 1: = = . (35)

Tad mēs uzreiz varam secināt, ka ( a 1 , a 2 , a 3) ½½ l o, ( b 1 , b 2 , b 3) ½½ l 1 , A o( x o, y o, z o)Î l o, A 1 (x 1 , y 1 , z 1)О l 1 . Izveidosim matricu

x 1 – x o y 1 – y o z 1 –z o

A = a 1 a 2 a 3 ,

b 1 b 2 b 3

un lai D = det A.

Teorēma 8.1.Leņķi starp l un p aprēķina pēc formulas

cos a = = . (36)

2. Taisns l o un l 1 krustojasÛ D ≠ 0.

3. Taisns l o un l 1 krustojasÛ D = 0 un nav kolineārs.

4. l o½½ l 1 rangs A= 2 un ½½.

5. l o = l 1 rangs A = 1.

Pierādījums. 1. Leņķis a starp taisnēm l o un l 1 var būt vienāds ar leņķi b starp to virziena vektoriem vai var būt tam blakus. Pirmajā gadījumā

cos a = cos b = ,

un otrajā gadījumā

cos a = – cos b =½ cos b½ = .

Šī formula attieksies arī uz pirmo gadījumu. Lūdzu, ņemiet vērā, ka zīmējumā nav redzama taisna līnija l o , un tai paralēlā taisne l o ¢ .

2, 3. Skaidrs, ka taisni l o un l 1 nav paralēli tad un tikai tad, ja to virziena vektori nav kolineāri. Šajā gadījumā taisnes atrodas vienā plaknē un krustojas - vektori ir koplanāri - to jauktais reizinājums ir vienāds ar nulli: = 0. Un koordinātēs šis precizitātes reizinājums ir vienāds ar D.

Attiecīgi, ja D ≠ 0, tad vektori nav koplanāri un līdz ar to taisni l o un l 1 neatrodas vienā plaknē Þ tie krustojas.

4, 5. Ja l o½½ l 1 vai l o = l 1, tad ½½. Bet pirmajā gadījumā vektors ir nekolineārs un līdz ar to arī matricas pirmā rinda A nesamērīgi ar otro un trešo rindu. Tātad rangs A = 2.

Otrajā gadījumā visi trīs vektori ir kolineāri viens pret otru un līdz ar to arī visas rindas

matricā A proporcionāls. Tātad rangs A = 1.

Un otrādi, ja || , tad taisni l o un l 1 paralēle vai sakritība; šajā gadījumā matricas otrā un trešā rinda A proporcionāls. Ja, tajā pašā laikā, rangs A= 2, tad matricas pirmā rinda ir nesamērīga ar otro un trešo, kas nozīmē, ka vektors nav kolineārs un Û l o || l 1 . Ja rangs A= 1, tad visas matricas rindas A ir proporcionāli, kas nozīmē, ka visi trīs vektori ir kolineāri viens pret otru Û l o = l 1 .

9. teorēma.Ļaujiet divām taisnēm l o un l 1 telpā ir doti ar to kanoniskajiem vienādojumiem (35). Tad

1. ja l o½½ l 1 , tad attālums starp l o un l 1 tiek atrasts pēc formulas

h = , (37)

2. ja l o un l 1 krustu, tad attālumu starp tiem nosaka pēc formulas

h = . (38)

Pierādījums. 1. Ļaujiet l o½½ l 1 . Uzzīmēsim vektoru no punkta A o , un uz vektoriem un konstruēsim paralelogramu. Tad tā augstums h būs attālums starp l o un l 1 . Šī paralelograma laukums ir: S=½ ´½, un bāze ir ½ ½. Tāpēc

h = S/½ ½ = (37).

2. Ļaujiet l o un l 1 ir šķērsoti. Zīmēsim caur taisnu līniju l o plakne p o ½½ l 1, un caur taisnu līniju l 1 uzzīmējiet plakni p 1 ½½ l o.

Tad kopējais perpendikulārs l o un l 1 būs kopīgs perpendikuls p o un p 1. Uzzīmēsim vektorus un no punkta A o un uz vektoriem, un konstruē paralēlskaldni. Tad tā apakšējā bāze atrodas p o plaknē, un tā augšējā bāze atrodas p 1 plaknē. Tāpēc paralēlskaldņa augstums būs kopīgs perpendikulārs p o un p 1, un tā vērtība h būs attālums starp l o un l 1 . Paralēlskaldņa tilpums ir ½ ½, un pamatnes laukums ir ½´½ Þ

h= V/S pamata = (38).

Sekas. Attālums no punkta A 1 (x 1 , y 1 , z 1) uz taisnu līniju l, ko dod vienādojums

aprēķina pēc formulas (37).

Problēmu risināšanas piemēri.

1. Dotas virsotņu A koordinātas(1,– 6), B(–3, 0), C(6, 9) trīsstūris ABC. Uzrakstiet vienādojumu riņķim ap trijstūri.

Risinājums. Lai izveidotu apļa vienādojumu, mums jāzina tā rādiuss R un centra koordinātas PAR(a, b). Tad vienādojums izskatās šādi:

(x–a) 2 +(y–b) 2 = R 2 .

Ap trijstūri norobežota riņķa centrs atrodas perpendikulāro bisektoru krustpunktā ar šī trijstūra malām. Viduspunktu koordinātu atrašana M 1 (x 1 , y 1), un M 3 (x 3 , y 3) malas B.C. Un AB attiecīgi:

x 1 = = = , y 1 = = = , M 1 .

Tāpat M 3 (–1,–3).

Ļaujiet l 3 – taisne, kas ir perpendikulāra bisektrisei AB, A l 1 līdz B.C.. Tad = (– 4, 6) ^ l 3 un l 3 iet cauri M 3. Tāpēc tā vienādojums ir:

– 4(x+1) + 6(y+3) = 0.

Tāpat = (9, 9)^ l 3. Tāpēc vienādojums l 1:

9(x-) + 9(y -) = 0

x + y – 6 = 0.

Mums ir PAR =l 1 I l 3. Tāpēc, lai atrastu punkta koordinātas PAR ir nepieciešams kopīgi atrisināt vienādojumus l 1 un l 3:

x + y – 6 = 0 ,

– 4x + 6y +14 = 0.

Pievienosim pirmo vienādojumu otrajam vienādojumam, kas reizināts ar 4:

x + y – 6 = 0,

10y – 10 = 0.

No šejienes y = 1, x = 5, O(5, 1).

Rādiuss ir vienāds ar attālumu no PAR uz kādu no trijstūra virsotnēm. Mēs atradām:

R =½½= = .

Tātad apļa vienādojums ir:

(x – 5) 2 + (y–1) 2 = 65.

2. Taisnstūra trīsstūrī ABC ir zināms vienas kājas vienādojums 3x – 2y + 5 = 0, virsotnes koordinātas C(–5,–5) un vidējā O koordinātas(– 3/2,–3)hipotenūza AB. Atrodiet koordinātas

virsotnes A, B un punkta E koordinātas, simetriski O attiecībā pret malu BC. Atrodiet trijstūra ABC mediānu krustpunkta koordinātas .

Risinājums. Lai ir tā kāja, kuras vienādojums mums ir dots ZA. To dod vispārīgs formas vienādojums

cirvis + autors + c = 0.

Šajā vienādojumā ģeometriskā nozīme

koeficienti a Un b ir normālā vektora koordinātas ( a, b). Tāpēc (3,-2)^ Sv.

Izveidosim perpendikula vienādojumu l = O.D. uz sāniem ZA un atrodiet punkta koordinātas D. Vektors būs paralēls O.D., t.i. tas ir šīs līnijas virziena vektors. Turklāt mēs zinām punkta koordinātas PAR uz šīs taisnās līnijas. Parametru vienādojuma sastādīšana l:

x = – + 3t, (*)

y = – 3 - 2t .

Mums ir D = l es B.C.. Tāpēc, lai atrastu šī punkta koordinātas, mums kopīgi jāatrisina vienādojumi l Un B.C.. Aizstāsim x Un y no Eq. l vienādojumā B.C.:

3(– + 3t) –2(–3 -2t)+5 = 0,

– + 9t +6 +4t+5 = 0,

13t = –, t D= – .

Aizstājiet to, ko atradām t vienādojumā l un atrodiet punkta koordinātas D(–3,–2). Lai atrastu koordinātas E Atcerēsimies taisnas līnijas parametriskā vienādojuma fizisko nozīmi: tas nosaka taisnu un vienmērīgu kustību. Mūsu gadījumā sākuma punkts ir PAR OE divreiz garāks par segmentu OD. Ja laikā t D= – esam tālu nogājuši PAR pirms tam D, tad ceļš no PAR pirms tam E ar laiku tiksim garām tE= 2t D= –1. Aizvietojot šo vērtību ar (*), mēs atrodam E(– 4,5;–1).

Punkts D sadala segmentu B.C. Uz pusēm. Tāpēc

x D = , y D = .

No šejienes mēs atrodam

x B= 2xD– xC= –1, y B = 2y D – y C =1, B(–1, 1).

Tāpat, izmantojot faktu, ka PAR– vidus AB, atrodiet punkta koordinātas A(-2,-7). Ir vēl viens veids, kā atrisināt šo problēmu: aizpildiet Δ ABC uz paralelogramu.

Vispārīgās formulas segmenta sadalīšanai šajā sakarā izskatās šādi:

x C = , y D = ,

ja punkts AR sadala segmentu AB attiecībā l 1:l 2, t.i. ½ A.C.½:½ B.C.½ = l 1: l 2.

Ir zināms, ka mediānu krustpunkts sadala mediānu proporcijā 2:1, skaitot no virsotnes. Mūsu gadījumā R sadala CO proporcijā 2:1. Tāpēc

xP = = = – ,

yP = = = – .

Atbilde:A(–2,–7), B(–1, 1), P.

3. Dotas virsotņu A koordinātas(– 4,–2), B(9, 7), C(2,– 4)trīsstūris ABC. Sastādiet bisektrise AD vispārīgo vienādojumu un atrodiet punkta D koordinātas.

Risinājums. No elementārās matemātikas kursa ir zināms, ka = . Mēs aprēķinām

(13, 9), (6,–2);

½½= = 5, ½½= = 2.

x D = = = 4,

y D = = = – , D(4,–).

Mēs sastādām taisnas līnijas vienādojumu, kas iet caur punktiem A Un D. Viņai vektors ir ceļvedis. Bet mēs varam izmantot jebkuru kolineāro vektoru kā ceļvedi. Piemēram, būs ērti ņemt = , (7, 1). Tad vienādojums

AD: = y+ 2 Û x – 7y– 10 = 0.

Atbilde:D(4,–), AD: x – 7y– 10 = 0.

4. Doti divu mediānu x vienādojumi – y– 3 = 0, 5x + 4y– 9 = 0 trijstūris ABC un virsotnes A koordinātas(– 1, 2). Uzrakstiet trešās mediānas vienādojumu.

Risinājums. Vispirms mēs pārliecināmies, ka punkts A nepieder pie šīm mediānām. Trijstūra mediānas krustojas vienā punktā M. Tāpēc tie ir iekļauti līniju komplektā, kas iet cauri M. Izveidosim vienādojumu šim staram:

l( x – y– 3) + m(5 x + 4y– 9) = 0.

Koeficientus l un m nosaka līdz proporcionalitātei; tāpēc varam pieņemt, ka m = 1 (ja m = 0, tad staru kūļa vienādojums norāda tikai pirmo mediānu, un vēlamā taisne ar to nesakrīt). Mēs iegūstam staru vienādojumu:

(l + 5) x+ (–l + 4) y– 3l – 9 = 0.

No šī stara mums jāizvēlas taisna līnija, kas iet caur punktu A(- 12). Aizstāsim tās koordinātas stara vienādojumā:

– (l + 5) + 2 (–l + 4) – 3l – 9 = 0,

– 6l – 6 = 0, l = –1.

Atrasto l vērtību aizstājam staru kūļa vienādojumā un iegūstam vēlamo vidējo vienādojumu:

4x + 5y– 6 = 0.

Atbilde: 4x + 5y– 6 = 0.

5. Dotas trīsstūrveida piramīdas SABC virsotņu koordinātas: A(–3, 7, 1), B(–1, 9, 2), C(–3, 6, 6) S(6,–5,–2). Uzrakstiet pamatplaknes ABC vienādojumu un augstuma SD vienādojumu. Atrodiet punkta D un punkta S koordinātas¢ , simetrisks S attiecībā pret pamatnes plakni.

Risinājums. Atradīsim divu vektoru koordinātas, kas ir paralēlas bāzes plaknei p = ABC:

= (2, 1, 1), = (0,–1, 5).

Vienādojums plaknei, kas iet caur noteiktu punktu A(x o, y o, z o) paralēli diviem nekolineāriem vektoriem ( a 1 ,a 2 , a 3), (b 1 ,b 2 , b 3) ir forma

x – x o y – y o z – z o

a 1 a 2 a 3 = 0.

b 1 b 2 b 3

Mēs aizstājam savus datus ar šo vienādojumu:

x + 3 y – 7 z – 1

2 2 1 = 0.

0 –1 5

Mēs paplašinām determinantu:

No plaknes vienādojuma mēs atklājam, ka vektors (11,–10,–2) ir plaknes normālais vektors. Tas pats vektors būs ceļvedis taisnei h = SD. Parametrisks vienādojums taisnei, kas iet caur noteiktu punktu A(x o, y o, z o) ar virziena vektoru ( a 1 ,a 2 , a 3) ir forma

x = x o + a 1 t ,

y = y o + a 2 t ,

z = z o + a 3 t .

Mūsu gadījumā mēs iegūstam vienādojumu:

x = 6 + 11t ,

h: y = –5 – 10t , (*)

z = –2 – 2t .

Atradīsim perpendikula pamatu. Tas ir taisnes krustpunkts ar plakni p. Lai to izdarītu, mums kopā jāatrisina vienādojumi un p. Aizstāšana no vienādojuma lπ vienādojumā:

11(6 + 11t) – 10(–5 – 10 t) – 2(–2 – 2t) + 105 = 0,

66 + 121 t + 50 + 100 t + 4 + 4 t + 105 = 0,

225 y = –225, t = –1.

Atrasts t aizstāt vienādojumā l un atrodiet koordinātas D(–5, 5, 0).

Atcerēsimies taisnas līnijas parametriskā vienādojuma fizisko nozīmi: tas nosaka taisnu un vienmērīgu kustību. Mūsu gadījumā sākuma punkts ir S, ātruma vektors ir. Līnijas segments SS¢divreiz garāks par segmentu SD un tas prasīs divreiz ilgāku laiku, lai to pabeigtu. Ja laikā t D= – 1 mēs esam aizgājuši no S pirms tam D, tad ceļš no S pirms tam S¢ mēs iesim cauri laikam t¢ = 2 t D= –2. Aizstājot šo vērtību ar (*), mēs atrodam S¢(–16, 15; 2).

Atbilde:ABC: 11x – 10y– 2z +105 = 0, D(–5, 5, 0), S¢(–16, 15; 2),

x = 6 + 11t ,

SD: y = –5 – 10t ,

z = –2 – 2t .

6. Doti ir plaknes p taisnes l vienādojumi:

Pārliecinieties, ka l un p krustojas, un izveidojiet vienādojumu l projekcijai¢ taisne l uz plakni. Atrodiet leņķi starp l un p .

Risinājums. No taisnes vienādojuma atrodam tās virziena vektoru: (1,–1, 2) un punktu uz šīs taisnes: A(6, 0, 2) , un no plaknes vienādojuma - plaknei normāls vektors:

(5,–2, 4). Acīmredzot, ja l½½ p vai , tad ^ t.i. · = 0. Pārbaudīsim:

· = 5 1–2 (–1) + 4 2 = 15 ¹ 0.

nozīmē, l krustojas ar π. Leņķis starp l un p tiek atrasti pēc formulas:

grēks a = ;

|| = = , || = = = 3 .

grēks a = = .

Ļaujiet A o – punktu projekcija A lidmašīnā un B = l es π . Tad l¢= A o B ir taisnas līnijas projekcija. Vispirms noskaidrosim punkta koordinātas B. Lai to izdarītu, mēs pārrakstām taisnās līnijas vienādojumu l parametru formā:

x = 6 + t,

l: y = – t,

z = 2 + 2t,

un atrisiniet to kopā ar plaknes vienādojumu π . Aizstāšana no vienādojuma l vienādojumā π :

5(6 + t) – 2(– t) + 4(2 + 2t) + 7 = 0,

30 + 5t + 2t + 8 + 8t + 7 = 0,

15t = – 45, t = – 3.

Aizstājot šo t vienādojumā l atrast koordinātas B(3, 3, 4). Izveidosim perpendikula vienādojumu h = A.A. o. Pa taisno h vektors kalpo kā ceļvedis. Tāpēc h ko dod vienādojums

x = 6 + 5t,

h: y = –2 t,

z = 2 + 4t,

Mēs to atrisinām kopā ar π plaknes vienādojumu, lai atrastu punkta koordinātas A o:

5(6 + 5t) – 2(–2t) + 4(2 + 4t) + 7 = 0,

30 + 25t + 4t + 8 + 16t + 7 = 0,

45t = – 45, t = – 1.

Aizstāsim šo t vienādojumā h un atrodam A o (1, 2,–2). Līnijas virziena vektora atrašana l": A o B(2, 1,–2) un iegūstiet tā vienādojumu:

.

7. Taisni l telpā dod vienādojumu sistēma

2x+2y– z– 1=0,

4x– 8y+ z – 5= 0,

un ir dotas punkta A koordinātas(–5,6,1). Atrodiet punkta B koordinātas, kas ir simetriskas pret A attiecībā pret taisni l.

Risinājums.Ļaujiet P– no punkta nomests perpendikula pamats A tieši l. Vispirms atradīsim punkta koordinātas P. Lai to izdarītu, mēs izveidosim vienādojumu plaknei p, kas iet caur punktu A perpendikulāri plaknēm p 1 un p 2. Mēs atrodam normālos vektorus šīm plaknēm: (2, 2,–1), (4,–8, 1). Plaknei p tie būs ceļveži. Tāpēc šīs plaknes vienādojums ir:

x + 5 y – 6 z – 1

2 2 –1 = 0.

4 –8 1

– 6(x + 5) – 6(y – 6) –24(z – 1) = 0 .

Pirms iekavas atvēršanas noteikti

Vispirms visu vienādojumu sadaliet ar – 6:

x + 5 + y – 6 + 4(z – 1) = 0,

x+ y+ 4z – 5 = 0.

Tagad P– plakņu p, p 1 un p 2 krustošanās punkts. Lai atrastu tās koordinātas, mums jāatrisina sistēma, kas sastāv no šo plakņu vienādojumiem:

x + y + 4z – 5 = 0,

4x – 8y + z – 5 = 0,

2x + 2y – z – 1 = 0.

Atrisinot to, izmantojot Gausa metodi, mēs atrodam P(1,0,1). Tālāk, izmantojot faktu, ka P– vidus AB atrodam punkta koordinātas B(7,–6,1).

Punkts P var atrast citā veidā, vistuvāk A taisnas līnijas punkts l. Lai to izdarītu, šai līnijai ir jāizveido parametru vienādojums. Kā tas tiek darīts, skatiet uzdevumu 10 . Par turpmākajām darbībām skatiet uzdevumu 8 .

8. IN D ABC ar virsotnēm A(9, 5, 1), B(–3, 8, 4), C(9,–13,–8) augstums AD ir uzzīmēts. Atrodiet punkta D koordinātas, uzrakstiet līnijas AD vienādojumu, aprēķināt h=½ AD½ un pārbaudiet h, aprēķinot S D ABC, izmantojot krustojumu.

Risinājums. Acīmredzot būtība D var atrast šādi: D= π I B.C., kur π ir plakne, kas iet caur punktu A perpendikulāri sāniem B.C.. Šai plaknei kalpo kā parastais vektors. Mēs atrodam (12,–21,–12). Šī vektora koordinātas pilnībā dalās ar 3. Tāpēc par p normālu vektoru varam ņemt = , (4,–7,–4). Vienādojums plaknei π, kas iet caur punktu A o( x o, y o, z o) perpendikulāri vektoram ( a, b, c), ir šāda forma:

a(x – x o) + b(y – y o) + c(z – z o) = 0.

Mūsu gadījumā:

4(x – 9) - 7(y – 5) - 4(z – 1) = 0,

4x - 7y - 4z + 3 = 0,

Izveidosim taisnas līnijas vienādojumu B.C.. Viņai vektors būs ceļvedis:

x = –3 + 4t,

B.C.: y = 8 – 7t, (*)

z = 4 – 4t,

Tāpēc ka D= π I B.C., lai atrastu punkta koordinātas D vienādojumi ir jāatrisina kopā π Un B.C.. Aizstāšana no vienādojuma B.C.π vienādojumā:

4(–3 + 4t) – 7(8 – 7t) – 4(4 – 4t) + 3 = 0,

–12 + 16 t – 56 + 49t – 16 + 16 t + 3 = 0,

81t = 81, t = 1.

Aizstāsim šo t līnijas vienādojumā B.C. un atrodam D(1, 1, 0). Tālāk, zinot punktu koordinātas A Un D, mēs sastādām taisnās līnijas vienādojumu AD Mēs aprēķinām attālumu starp punktiem, izmantojot formulu:

i j k i j k

´ = –12 3 3 = –27· – 4 1 1 = –27(– i + 4j– 8k) .

0 –18 –9 0 2 1

(Aprēķinu procesā izmantojām determinanta īpašību: vienas rindas elementu kopējo koeficientu var izņemt no determinanta zīmes).

SΔ ABC= · 27 = .

No otras puses, S Δ ABC = | |· h. No šejienes h= . Mēs atradām

Tāpēc h= 9. Tas atbilst iepriekš atrastajai atbildei.

Punkts D var atrast vistuvāk A taisnas līnijas punkts B.C. izmantojot diferenciālrēķina metodes. Ļaujiet M(t) – patvaļīgs taisnes punkts B.C.; tās koordinātas nosaka sistēma (*):

M(–3 + 4t, 8 – 7t, 4 – 4t).

Attāluma kvadrātā atrašana no punkta A pirms tam M(t):

h 2 (t) = (9 + 3 – 4t) 2 + (5 – 8 + 7t) 2 + (1 – 4 + 4t) 2

= (12 – 4t) 2 + (–3 + 7t) 2 + (–3 + 4t) 2 =

144 – 96t + 16t 2 + 9 – 42t + 49t 2 + 9 – 24t + 16t 2 =

81t 2 – 162t + 162.

Atradīsim funkcijas mazāko vērtību h 2 (t) izmantojot atvasinājumu:

h 2 (t) = 162t – 162; h 2 (t) = 0 Þ t = 1.

Aizstājiet šo vērtību t līnijas vienādojumā B.C. un mēs to atrodam D(1, 1, 0) ir vistuvāk A punkts uz līnijas B.C..

9. Izpētiet šādu plakņu pāru relatīvo stāvokli(krustojas, paralēli, sakrīt). Ja plaknes krustojas, tad atrodiet leņķi starp tām, ja tās ir paralēlas – attālums starp tiem.

A). p1:2 y+ z + 5 = 0, p 2: 5 x + 4y– 2z +11 = 0.

Risinājums. Ja plaknes p 1 un p 2 ir dotas ar to vispārīgajiem vienādojumiem

a 1 x + b 1 y + c 1 z + d 1 = 0, a 2 x + b 2 y + c 2 z + d 2 = 0,

p 1 ½ ½ p 2 Û = = ¹ ,

p 1 = p 2 Û = = = .

Mūsu gadījumā ¹ ¹, tāpēc plaknes nav paralēlas un nesakrīt. Tas nozīmē, ka tie krustojas. Leņķi starp plaknēm aprēķina pēc formulas

cos a = ,

kur un ir šo plakņu normālie vektori. Mūsu gadījumā

(0, 2, 1), (5, 4,–2), · = 0,5 + 2 · 4 + 1 · (–2);

|| = = , || = = 3 .

Tātad cos a = = .

Atbilde: a = arccos.

b) p1: x – y+ 2z + 8 = 0,

p2:2 x – y+ 4z –12 = 0.

Risinājums. Paralēlitātes vai sakritības pārbaude:

Tas nozīmē p 1 ½ ½ p 2, bet p 1 ¹ p 2 . Attālums no punkta A(x, y, z) uz vienādojuma norādīto plakni atrod pēc formulas

h = .

Izvēlēsimies punktu AОp 1 . Lai to izdarītu, jums ir jāizvēlas jebkuras trīs koordinātas, kas atbilst vienādojumam p 1. Mūsu gadījumā visvienkāršākā lieta ir: A o (0, 8, 0). Attālums no A o līdz p 2 un būs attālums starp p 1 un p 2:

h = = .

10. Izveidojiet plaknes vienādojumu p, kas sadala uz pusēm vienu no divšķautņu leņķiem starp plaknēm

p1:2 x– y+ 2 = 0, p 2: 5 x+ 4y– 2z–14 = 0,

kas satur šo punktu A(0, 3,–2). Sastādiet taisnes l parametrisku vienādojumu = lpp 1 I lpp 2 ;

Risinājums. Ja punkts atrodas uz plaknes p, kas sadala divskaldņa leņķi, tad attālumi h 1 un h 2 no šī punkta līdz p 1 un līdz p 2 ir vienādi.

Mēs atrodam šos attālumus un pielīdzinām tiem:

Varam atvērt moduļus ar vienādām vai dažādām zīmēm. Līdz ar to varam iegūt 2 atbildes, jo... p 1 un p 2 veido divus divšķautņu leņķus. Bet nosacījums prasa atrast vienādojumu plaknei, kas sadala leņķi, kurā punkts atrodas A. Tātad punkta koordinātas M aizvietojot šo plakņu vienādojumu kreisajā pusē lpp 1, un tām jābūt tādām pašām zīmēm kā punkta koordinātām A. Ir viegli pārbaudīt, vai šīs zīmes ir p 1 un “+” p 2. Tāpēc mēs paplašinām pirmo moduli ar “–” zīmi, bet otro ar “+” zīmi:

3(-2x + y- 2) = 5x+ 4y– 2z–14,

p:11 x + y - 2z - 14 = 0.

Lai izveidotu taisnas līnijas vienādojumu l, mums jāatrod šīs līnijas virziena vektors un punkts uz tās.

No vienādojumiem p 1 un p 2 atrodam normālvektoru koordinātas šīm plaknēm: (2,–1, 0), (5, 4,–2). Tiešais vektors l perpendikulāri un To var atrast, izmantojot vektora reizinājumu (pēc definīcijas, ja = ´, tad ^ un ^):

= ´ = 2–1 0 = 2 i + 4j+ 13k .

Lai atrastu viena punkta koordinātas taisnē, mums jāatrod konkrēts vienādojumu sistēmas risinājums

Tā kā ir divi vienādojumi un trīs nezināmie, sistēmai ir bezgalīgi daudz risinājumu. Viss, kas mums jādara, ir izvēlēties vienu. Vienkāršākais veids ir likt x= 0 un tad mēs atrodam

Þ z = – 3, .

Kanoniskais vienādojums taisnei, kas iet caur punktu B(x o, y o, z o) paralēli vektoram ( a 1 , a 2 , a 3), ir šāda forma:

Mūsu gadījumā mums ir vienādojums:

l: = = .

Atbilde: lpp: 11 x + y – 2z = 0, l: = = .

11. Doti divu līniju vienādojumi telpā:

x = –1 – t, x = –3 + 2t¢,

l 1: y = 6 + 2 t, l 2: y = –2 – 3t¢,

z = 5 + 2t, z = 3 – 2t¢.

Pierādiet, ka šīs taisnes krustojas, un izveidojiet vienādojumu to kopējam perpendikulam.

Risinājums. No taisnu vienādojumiem atrodam to virziena vektoru koordinātas: (–1, 2, 2), (2,–3,–2) un punktu l 1, kas nozīmē, ka tas ir kopīgā perpendikula virziena vektors. šīs līnijas. Mēs jau esam atraduši tās koordinātas: (2, 2,–1). Lai

uzrakstiet vienādojumu h mums jāatrod viena punkta koordinātas šajā taisnē. Lai to izdarītu, mēs izveidosim vienādojumu plaknei π, kas iet cauri l 1 un h. Viņai vektori būs ceļveži, un AÎp.

x – 1 y – 2 z – 1

– 6(x – 1) + 3(y – 2) – 6(z – 1) = 0.

– 2(x – 1) + (y – 2) – 2(z – 1) = 0.

p: –2 x + y – 2z + 2 = 0.

Krustojuma punkta atrašana l 2 un π. Lai to izdarītu, no vienādojuma l 2 vienādojumā aizstājam π:

–2(–3 + 2t¢) –2 + 3 t¢ – 2 (3 – 2 t¢) + 2 = 0,

6 – 4t¢ – 2 – 3 t¢ – 6 – 4 t¢ + 2 = 0,

–7t¢= 0, t¢= 0.

Aizstājiet to, ko atradām t¢ iekšā

Jūsu privātuma saglabāšana mums ir svarīga. Šī iemesla dēļ mēs esam izstrādājuši Privātuma politiku, kurā aprakstīts, kā mēs izmantojam un uzglabājam jūsu informāciju. Lūdzu, pārskatiet mūsu privātuma praksi un informējiet mūs, ja jums ir kādi jautājumi.

Personiskās informācijas vākšana un izmantošana

Personiskā informācija attiecas uz datiem, kurus var izmantot, lai identificētu vai sazinātos ar konkrētu personu.

Jums var tikt lūgts sniegt savu personisko informāciju jebkurā laikā, kad sazināsieties ar mums.

Tālāk ir sniegti daži piemēri par to, kāda veida personas informāciju mēs varam vākt un kā mēs varam izmantot šādu informāciju.

Kādu personas informāciju mēs apkopojam:

• Kad jūs iesniedzat pieteikumu vietnē, mēs varam apkopot dažādu informāciju, tostarp jūsu vārdu, tālruņa numuru, e-pasta adresi utt.

Kā mēs izmantojam jūsu personisko informāciju:

• Mūsu apkopotā personas informācija ļauj mums sazināties ar jums par unikāliem piedāvājumiem, akcijām un citiem pasākumiem un gaidāmajiem pasākumiem.
• Laiku pa laikam mēs varam izmantot jūsu personisko informāciju, lai nosūtītu svarīgus paziņojumus un paziņojumus.
• Mēs varam izmantot personas informāciju arī iekšējiem mērķiem, piemēram, auditu, datu analīzes un dažādu pētījumu veikšanai, lai uzlabotu mūsu sniegtos pakalpojumus un sniegtu jums ieteikumus par mūsu pakalpojumiem.
• Ja jūs piedalāties balvu izlozē, konkursā vai līdzīgā akcijā, mēs varam izmantot jūsu sniegto informāciju šādu programmu administrēšanai.

Informācijas izpaušana trešajām personām

Mēs neizpaužam no jums saņemto informāciju trešajām personām.

Izņēmumi:

• Ja nepieciešams - saskaņā ar likumu, tiesas procedūru, tiesvedībā un/vai pamatojoties uz publiskiem pieprasījumiem vai valdības iestāžu lūgumiem Krievijas Federācijas teritorijā - izpaust savu personas informāciju. Mēs varam arī izpaust informāciju par jums, ja konstatēsim, ka šāda izpaušana ir nepieciešama vai piemērota drošības, tiesībaizsardzības vai citiem sabiedriski svarīgiem mērķiem.
• Reorganizācijas, apvienošanas vai pārdošanas gadījumā mēs varam nodot mūsu apkopoto personas informāciju attiecīgajai trešajai pusei.

Personiskās informācijas aizsardzība

Mēs veicam piesardzības pasākumus, tostarp administratīvus, tehniskus un fiziskus, lai aizsargātu jūsu personisko informāciju pret pazaudēšanu, zādzību un ļaunprātīgu izmantošanu, kā arī no nesankcionētas piekļuves, izpaušanas, pārveidošanas un iznīcināšanas.

Jūsu privātuma ievērošana uzņēmuma līmenī

Lai nodrošinātu jūsu personiskās informācijas drošību, mēs saviem darbiniekiem paziņojam par privātuma un drošības standartiem un stingri īstenojam privātuma praksi.

Šajā rakstā mēs sapratīsim taisnas līnijas jēdzienu trīsdimensiju telpā, apsvērsim līniju relatīvās pozīcijas iespējas un pakavēsimies pie galvenajām taisnas līnijas noteikšanas metodēm telpā. Labākai izpratnei mēs piedāvājam grafiskas ilustrācijas.

Lapas navigācija.

Taisna līnija telpā ir jēdziens.

Pēc tam, kad esam devuši paralēlu līniju definīciju telpā, mums vajadzētu runāt par taisnes virziena vektoriem to nozīmīguma dēļ. Jebkurš vektors, kas nav nulle, kas atrodas uz šīs taisnes vai taisnes, kas ir paralēla tai, tiks saukts par taisnes virziena vektoru. Taisnes virziena vektoru ļoti bieži izmanto, risinot problēmas, kas saistītas ar taisnu līniju telpā.

Visbeidzot, divas līnijas trīsdimensiju telpā var krustoties. Divas līnijas telpā sauc par šķībām, ja tās neatrodas vienā plaknē. Šī divu līniju relatīvā pozīcija telpā noved pie jēdziena par leņķi starp krustojošām līnijām.

Metodes taisnas līnijas noteikšanai telpā.

Ir vairāki veidi, kā unikāli noteikt taisnu līniju telpā. Uzskaitīsim galvenos.

No aksiomas mēs zinām, ka taisne iet caur diviem punktiem un tikai vienu. Tādējādi, ja mēs atzīmēsim divus punktus telpā, tas ļaus mums nepārprotami noteikt taisni, kas iet caur tiem.

Ja trīsdimensiju telpā tiek ieviesta taisnstūra koordinātu sistēma un tiek norādīta taisne, norādot tās divu punktu koordinātas, tad mums ir iespēja izveidot vienādojumu taisnei, kas iet caur diviem dotiem punktiem.

Otrā metode līnijas definēšanai telpā balstās uz teorēmu: caur jebkuru telpas punktu, kas neatrodas uz noteiktas taisnes, iet taisne, kas ir paralēla dotajai, un tikai viena.

Tādējādi, ja mēs norādām taisni (vai šīs līnijas nogriezni) un punktu, kas uz tās neatrodas, tad mēs unikāli definēsim taisni, kas ir paralēla dotajai un iet caur doto punktu.

Varat norādīt punktu, caur kuru līnija iet, un tās virziena vektoru. Tas arī ļaus jums nepārprotami noteikt taisnu līniju.

Ja taisne ir norādīta šādā veidā attiecībā pret fiksētu taisnstūra koordinātu sistēmu, tad uzreiz varam pierakstīt tās kanoniskos taisnes vienādojumus telpā un parametriskos taisnes vienādojumus telpā.

Sekojošā metode līnijas definēšanai telpā balstās uz stereometrijas aksiomu: ja divām plaknēm ir kopīgs punkts, tad tām ir kopēja taisne, uz kuras atrodas visi šo plakņu kopīgie punkti.

Tādējādi, definējot divas krustojošas plaknes, mēs unikāli definējam taisnu līniju telpā.

Vēl viens veids, kā definēt līniju telpā, izriet no teorēmas (tās pierādījumu varat atrast grāmatās, kas uzskaitītas šī raksta beigās): ja ir dota plakne un punkts, kas tajā neatrodas, tad iet viena taisne. caur šo punktu un perpendikulāri dotajai plaknei .

Tādējādi, lai noteiktu taisnu līniju, varat norādīt plakni, kurai vēlamā taisne ir perpendikulāra, un punktu, caur kuru šī taisne iet.

Ja taisne ir norādīta šādā veidā attiecībā pret ieviesto taisnstūra koordinātu sistēmu, tad būs noderīgi zināt raksta materiālu par taisnes vienādojumu, kas iet caur noteiktu punktu perpendikulāri noteiktai plaknei.

Bibliogrāfija.

• Atanasjans L.S., Butuzovs V.F., Kadomcevs S.B., Pozņaks E.G., Judina I.I. Ģeometrija. 7. – 9. klase: mācību grāmata vispārējās izglītības iestādēm.
• Atanasjans L.S., Butuzovs V.F., Kadomcevs S.B., Kiseļeva L.S., Pozņaka E.G. Ģeometrija. Mācību grāmata vidusskolas 10-11 klasēm.
• Bugrovs Ya.S., Nikolsky S.M. Augstākā matemātika. Pirmais sējums: lineārās algebras un analītiskās ģeometrijas elementi.
• Iļjins V.A., Pozņaka E.G. Analītiskā ģeometrija.

Autortiesības pieder gudriem studentiem

Visas tiesības aizsargātas.
Aizsargā autortiesību likums. Nevienu vietnes daļu, tostarp iekšējos materiālus un izskatu, nedrīkst reproducēt vai izmantot bez iepriekšējas rakstiskas autortiesību īpašnieka atļaujas.